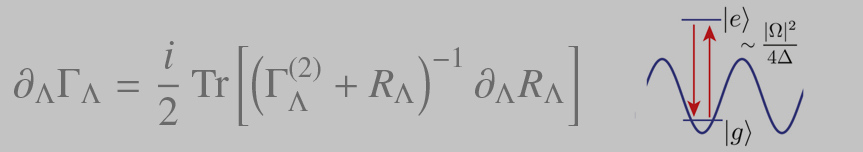
Summer Term 2024

14756.2024 | Advanced Quantum Mechanics

Lectures

Tuesday 8:00-9:30 in Lecture Hall III
Wednesday 12:00-13:30 in Lecture Hall III
The first lecture will be on the 9th of April.

Tutorials
Tutorials will be held on Thursdays.

There is a Slack workspace on which we will share all relevant information about the lecture. To register, please take a look at the information sheet . To access it, you need to be connected to the university network via VPN: see details on the RRZK website.

Contact:
Dr. Johan Aberg (johan.aberg [at] uni-koeln [dot] de)

Lecture Materials
Information sheet

Contents
Scattering theory: Scattering cross section; Lippmann-Schwinger equation, Green’s function, T- and S-matrix; optical theorem; Born approximation; centrosymmetric potential scattering, low energy scattering and scattering length, ultracold atom scattering and Feshbach resonances; time reversal in quantum mechanics (scattering theory is more fun than you might guess!).
Canonical Quantization: Qubits and electromagnetic fields: Physics and quantization of superconducting circuits, driven systems, rotating frame transformation, reduction to qubit Hamiltonian; quantization of classical electrodynamics coupled to non-relativistic matter, reduction to Jaynes-Cummings model, semiclassical limit, Rabi oscillation revivals, spontaneous emission and irreversible decay, inelastic light scattering.
Second Quantization: Bosons and fermions: Indistinguishable particle postulate, bosons and fermions, many-particle Hilbert space and Fock space; Representation of single- and two-particle operators in Fock space; quantum dynamics of field operators; applications: Bose-Einstein condensation of weakly interacting ultracold bosonic atoms, Gross-Pitaevskii equation and Bogoliubov theory; quantum phase transition of fermions and spins in one dimension.
Relativistic quantum mechanics and Dirac equation: Recap on special relativity and Lorentz group; Klein-Gordon equation; gauge invariance; Dirac equation: solutions and interpretation; non-relativistic limit; quantization of the Dirac field.

Literature
Is specified in the script.