 Der Bethe-Ansatz Der Bethe-Ansatz
|
Der Bethe-Ansatz wurde 1931 von Bethe eingeführt [1] und
ermöglicht Eigenwerte und Eigenvektoren vieler eindimensionaler
quantenmechanischer Vielteilchenmodelle exakt zu bestimmen.
Die Methode findet eine breite Anwendungsmöglichkeit, ist jedoch
sehr 'technisch'. Aus diesem Grund wird hier anhand des sogenannten
Spin-1/2 Heisenbergmodells nur die Grundidee übermittelt. Doch zuvor noch
einige Wort zum Modell selbst.
Einige Jahre nach Einführung der Quantenmechanik haben Heisenberg
und Dirac herausgefunden, dass die Wechselwirkung zwischen
Elektronenspins eine bedeutende Rolle in der Theorie des Ferromagnetismus
spielt [2]. Zur Beschreibung der Theorie wurde ein effektiver Hamiltonopperator
herangezogen (siehe Abbildung), dessen Austauschwechselwirkung Jij
durch die Coulomb-Abstoßung und das Pauli-Prinzip verursacht wird.
|
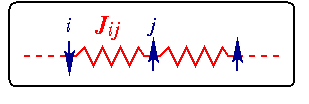
Die Abbildung verdeutlicht eine mögliche Spin-Konfiguration auf einem
eindimensionalen Gitter mit der Austauchswechselwirkung Jij
zwischen den Gitterplätzen i und j. Der effektive Hamiltonian wird
aus den Termen -JijSiSj
gebildet.
| 
|
In der Praxis wird oft der isotrope Fall untersucht, d.h. für alle
Gitterplätze hat man Jij=J zu setzen.
Das Heisenbergmodell ist rotationsinvariant, d.h. [H,Stot]=0,
wodurch alle Basiszustände nach der Quantenzahl
Stot=S(1)+...+S(N)=N/2-r sortiert werden können. Die Variable
N entspricht der Gittergröße und r beschreibt die Anzahl der
'geflippten' Spins.
Der Unterraum r=0 (alle Spins weisen in eine Richtung hin) besteht aus dem
einzigen Eigenzustand |F) = |+1...+N). Die Energie
E0=-JN/4 folgt unmittelbar aus der Schrödingergleichung
H|F) = E|F).
Wird nun ein Spin geflippt (r=1),
so läßt sich der Grundzustand aus der Superposition der N
translationsinvarinaten Eigenvektoren |n) = S-(n)|F)
(mit n=1,...,N) darstellen:
|P) = a1|1)+a2|2)+...+aN|N).
Man findet eine Lösung der Schrödingergleichung H|P) = E|P), wenn
an für alle n die Bedingung
2[E-E0]an = J[2an-an-1
-an+1]
erfüllt. Mit periodischen Randbedingungen, d.h.
an+N=an, gibt es insgesamt N verschiedene Lösungen
an = eikn mit k=2m*Pi/N und m=0,1,...,N-1. Die Energie
E-E0 = J(1-cos k)
erhält man direkt aus der oberen Gleichung.
Die nun folgenden Überlegungen gelte auch für den allgemeinen Fall
mit einer beliebigen Anzahl von geflippten Spins!
Bei zwei geflippten Spins (r=2) wird der Unterraum von N(N-1)/2 Basisvektoren
|n1n2) =
S-(n1)S-(n2)|F) aufgespannt. Der
Grundzustand hat dabei die Form
|P) = a1112|1112)+...+
aN1N2|N1N2),
wobei 1<=nn<=nn+1<=N für alle n=1,..,N-1 gelten
muss. Das Eigenwertproblem führt nun auf insgesamt N(N-1)/2 Gleichungen.
Hier ist es jedoch nützlich die Koeffizienten in der Darstellung
an1n2 =
Aei(k1n1+k2n2)
+ Bei(k1n1+k2n2)
zu wählen, die als Wellenfunktionen zwei superpositionierter Magnonen
(Spinwellen) zu interpretieren sind. Die recht aufwendige Untersuchung
(die Schritte werden hier nicht mehr präsentiert) liefert
schließlich die sogenannten Bethe-Quantenzahlen, die die Energie und den
Eigenzustand bestimmen.
Literatur:
| [1] |
H. Bethe, Z. Phys. 71, 205 (1931) |
| [2] |
W. Heisenberg, Z. Phys. 38, 441 (1926);
P. Dirac, Proc. Roy. Soc. London 112A, 661 (1926) |
Christian Dziurzik
2000-04-11
 Der Bethe-Ansatz
Der Bethe-Ansatz
 Der Bethe-Ansatz
Der Bethe-Ansatz
