 Numerische Methoden
Numerische Methoden
 Numerische Methoden Numerische Methoden
|
Numerische Zugänge haben also das Ziel, einen konkret vorgegeben Hamiltonoperator zu diagonalisieren. Dieses Verfahren wird als exakte Diagonalisierung bezeichnet. Trotz der oben diskutierten Vorteile in einer Dimension stellen bereits sehr kleine Systeme ein aufwendiges mathematisches Problem dar. Zur Illustration betrachten wir eine Kette der Länge L aus Atomen, die den Spin 1/2 tragen. Der lokale Hilbertraum eines Gitterplatzes hat damit die Dimension zwei. Global gibt es also n=2L Zustände, und der Hamiltonoperator kann durch eine 2L x 2L-Matrix dargestellt werden.Entgegen naiver Erwartungen existieren in der Natur eine Reihe von Substanzen, die ausgeprägte 1D Strukturen aufweisen. So ordnen sich Atome z.B. in Ketten an, wobei die Wechselwirkung innerhalb der Kette um ein vielfaches stärker ist als senkrecht dazu. Das physikalische Verhalten dieser (quasi)-eindimensionalen Verbindungen lässt daher hervorragend durch 1D Systeme modellieren. Im Gegensatz zu Systemen in höheren Dimensionen dominieren in einer Dimension Quantenfluktuationen im Vergleich zu thermischen, insbesondere bei tiefen Temperaturen. Insofern bieten 1D Systeme ein hervorragendes Spielfeld, um quantenmechanische Effekte zu untersuchen. Die Komplexität wächst in einer Dimension "nur" mit der einfachen Potenz der Systemgrösse. Es ist daher leicht einzusehen, dass hier am ehesten eine Chance besteht, die mathematischen Schwierigkeiten in den Griff zu bekommen.
Für ein sehr kleines System der Länge L=20 bedeutet dies bereits eine grosse Anzahl von möglichen Zuständen, nämlich n=1048576. Der Hamiltonoperator enthält damit 240=1099511627776=1.0995 x 1012 Matrixelemente. Allein um den Hamiltonoperator in numerischer Double-Genauigkeit (d.h. 8-Byte Floating-Point Variablen) zu speichern benötigte man folglich etwa 10000 Giga-Bytes (!!!), was selbst heutige Grossrechner vor Probleme stellt. Dabei ist noch nicht berücksichtigt, dass diese Matrix diagonalisiert werden muss, also über eine Million Eigenwerte und Eigenvektoren zu bestimmen sind. In der Praxis kann man etwa durch die Ausnutzung von Erhaltungsgrössen den numerischen Aufwand reduzieren, dennoch ist die Länge L=20 eine obere Grenze. Experimentell vorliegende Systeme hingegen haben typischerweise eine lineare Ausdehnung von etwa L=108 Atomen. An eine direkte numerische Behandlung von Systemen dieser Grösse ist also überhaupt nicht zu denken.
Um überhaupt Ergebnisse aus exakten Diagonalisierungen nutzen zu können, muss man sich klar machen, wie sich die endliche Systemgrösse in den physikalischen Eigenschaften bemerkbar macht. Üblicherweise zeigen sich diese sogenannten finite-size Korrekturen als Terme der Ordnung 1/L im Vergleich mit dem unendlich grossen System. Wird dieses Verhalten bereits für kleine Systemgrössen sichtbar, so kann der thermodynamische Limes daraus extrapoliert werden. In vielen Fällen reichen dazu Systeme mit L<100 jedoch nicht aus. Insbesondere bei tiefen Temperaturen führt das aus der endlichen Hamiltonmatrix stammende diskrete Spektrum aufgrund der s.g. finite-size Lücke auch qualitative zu Diskrepanzen in Systemen mit lückenloser Dispersion.
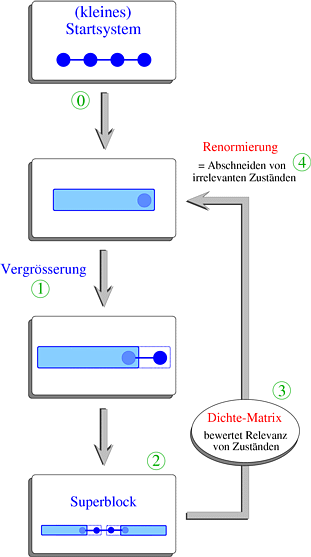
Ein sehr effizientes und überaus genaues Verfahren zum Erreichen grösserer Systeme stellt die Dichte-Matrix-Renormierungs-Gruppe (DMRG) dar, die auf S. White [1] zurück geht. Da grosse Kettenlängen, wie oben eindrucksvoll gezeigt, nicht direkt zugänglich sind, verfolgt man eine sehr einfache Idee. Anstelle direkt ein grosses System zu betrachten, startet man mit einer Grösse, die problemlos numerisch zu behandeln ist. Im folgenden wird das System iterativ vergrössert und nach jedem Anhängen von Gitterplätzen "unwichtige" Anteile herausprojeziert. Die folgende Grafik zeigt schematisch die Funktionsweise des s.g. infinite-size DMRG-Algorithmus.
|
Wir stellen uns eine Kette aus Spins der Länge s vor, wobei jeweils zwei benachbarte miteinander wechselwirken. Das einfachste Modell dieser Art ist etwa das Spin-1/2 Heisenberg-Modell. Ziel soll sein, die Grundzustandsenergie für ein möglichst grosses System zu bestimmen.
| 
|
Offensichtlich wird bei jedem Iterationsschritt die effektive Systemgrösse des Superblocks um zwei Spins erhöht. Man kann daher im Prinzip beliebige Systemgrössen erreichen. Bei jedem Renormierungsschritt jedoch erhöht sich aufgrund der Projektion der Fehler im Vergleich mit dem exakten Ergebnis. Dieser Prozess ist kumulativ. Glücklicherweise fallen die Gewichte der Blockzustände in der Regel exponentiell schnell ab, sodass man problemlos Kettenlängen von 100 und mehr erreicht. Die daraus abgeleiteten Grundzustandsenergien haben typischerweise Fehler <10-9 verglichen mit exakten Resultaten, was mit exakter Diagonalisierung nie zu erreichen wäre.
DMRG ist mittlerweile die beliebteste numerische Methode für eindimensionale Quantensysteme. Neben der sehr genauen Berechnung von Grundzustandsenergien können aber auch Erwartungswerte von Operatoren, wie z.B. die Magnetisierung, Korrelationsfunktionen und Energielücken sehr präzise ausgerechnet werden. Desweiteren ermöglicht eine neue Variante, die s.g. Transfer-Matrix DMRG (TMRG) [2,3] die Bestimmung von thermodynamischen Eigenschaften eindimensionaler Quantenmodelle, was mittlerweile in vielen Anwendungen bewiesen wurde. Die DMRG kann auch für zweidimensionale klassische Spin-Modelle, im Rahmen von stochastischen Prozessen und für diverse andere Probleme eingesetzt werden [4]
Literatur:
| [1] | S. R. White, Phys. Rev. Lett. 69, 2863 (1992); Phys. Rev. B 48, 10345 (1993) |
| [2] | X. Wang and T. Xiang, Phys. Rev B 56, 5061 (1997) |
| [3] | N. Shibata, J. Phys. Soc. Jap. 66, 2221 (1997) |
| [4] | Lecture Notes in Physics edited by I. Peschel et al. (Springer, Berlin, 1999), Vol. 528 |
Rainer Raupach