Computerphysik - numerische Methoden zur Lösung physikalischer Probleme

       

Dozent: Prof. Dr. Johannes Berg
Übungen: Dipl.-Phys. Jasper Franke


Eine große Zahl physikalischer Probleme führt auf Gleichungen, die nicht in geschlossener Form gelöst werden können. Numerische Verfahren spielen daher in den unterschiedlichsten Teilgebieten der Physik (Teilchen- und Festkörperphysik, Biophysik, Kosmologie, Meterologie) eine große Rolle. Diese Vorlesung bietet eine Einführung in die grundlegenden numerischen Methoden zur Lösung physikalischer Probleme, mit Anwendungen in der Mechanik, Elektrodynamik und Quantenmechanik.

Ziel ist auch die Entwicklung von Programmierfertigkeiten. Die Übungen sind kleine Programmierprojekte, in denen die in der Vorlesung diskutierten Konzepte praktisch implementiert werden. Die Abbildungen auf dieser Seite zeigen einige der Ergebnisse.

1. Elementare Numerik: Gleichungen und Integrale
2. Differentialgleichungen
3. Eigenwertprobleme
4. Zufallszahlen und Monte-Carlo Methoden

Die Vorlesung ist Teil der Pflichtveranstaltungen des Bachelor in Physik.

Vorausgesetzte Kenntnisse

Grundkenntnisse in einer Programmiersprache. Die Vorlesung nutzt die Sprache C. Das Rechenzentrum bietet einen Einführungskurs an, der vom 15.-26. März stattfindet. Weitere Informationen und ein Webformular zur Anmeldung sind unter diesem link zu finden (Kurs 12).

Es ist aber durchaus möglich sich die Grundkenntnisse im Programmieren selbst beizubringen, etwa mit der unten angegebenen Literatur und - wichtig - selbständigem Ausprobieren. Wenn Sie ein kleines Progamm schreiben können, das die ersten N Primzahlen generiert, sind Sie auf jeden Fall fit für den Kurs. Bei Zweifeln und Unsicherheiten können Sie sich vorab bei mir melden.

Termine

Vorlesungen: Montag 12:00-13:30 im Hörsaal III
Übungen: Termine und Ort finden Sie auf der Übungsseite
Klausur: 3.8.2010, 13:30-16:30, Hörsaal I
Nachklausur: 5.10.2010, 13:30, HS III

Literatur

Einführend und begleitend
T. Pang, An Introduction to Computational Physics, Cambridge University Press
P.L. DeVries, Computerphysik, Spektrum Akademischer Verlag

Weiterführend
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in C, Cambridge University Press

C-Programmierung
Einführend
H. Erlenkötter, C: Programmieren von Anfang an, Rowohlt Taschenbuch

Kompakt
B.W. Kernighan, D.M. Ritchie, The C Programming Language, Prentice Hall

Notizen zur Vorlesung, die von Gerold Busch aufgenommen wurden, stehen hier zur Verfügung.

Spielregeln und Ergebnisse

Scheinkriterium ist das Bestehen der Klausur zum Ende des Semesters. Die Zulassung zur Klausur erfordert regelmäßige Teilnahme an den Übungen. Details finden Sie auf der Übungsseite.

Die Liste der erfolgreichen Klausurteilnehmer, bezw. der letzten vier Stellen ihrer Matrikelnummer, ist hier. Klausurteilnehmer, die nicht auf dieser Liste stehen, sind zur Nachklausur zugelassen (s.o.), zu der wir Ihnen Erfolg wünschen. Einsicht in die Klausur können Sie am 17.9 um 15 Uhr nehmen (Seminarraum Theoretische Physik). Die Ergebnisse der Nachklausur sind hier, wieder mit den letzten 4 Stellen der Matrikelnummer und der Note. Für Klausureinsicht kontaktieren Sie bitte Herrn Franke.


Abbildungen

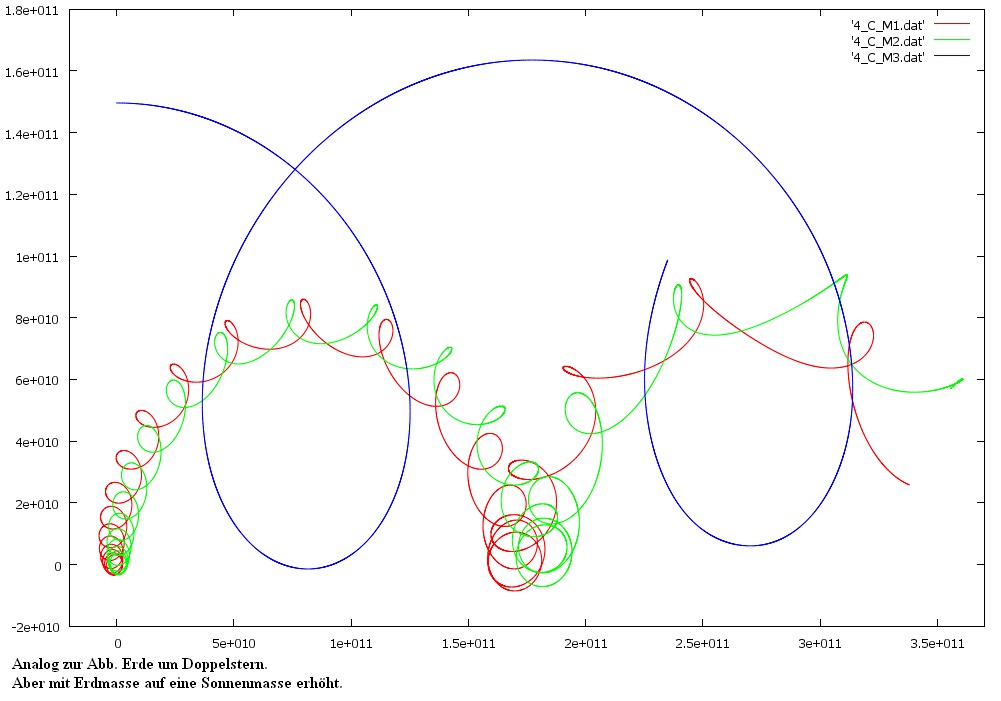
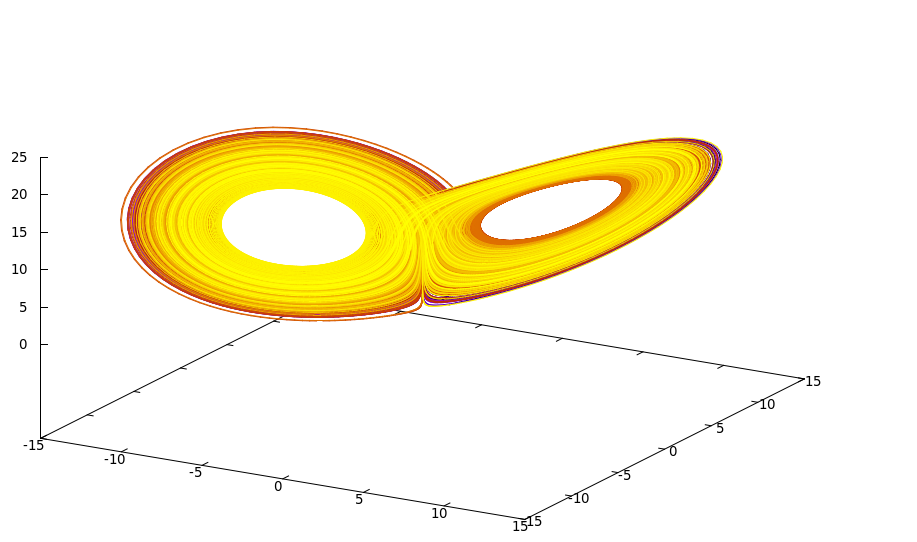
1. Diese Abbildung von Martin Sundermann zeigt die Dynamik eines Systems aus drei Sternen, siehe Übung 4.
2. Die Abbildung von Christoph Schultens zeigt den seltsamen Attraktor des Lorenz-Systems, siehe Übung 5.
3. Die Abbildung von Tilman Disselkamp zeigt das elektrische Potential einer Ladungsverteilung, die sich aus zwei Gaussverteilungen zusammensetzt.
Die Berechnung erfolgte mit der Relaxationsmethode, siehe Übung 6.
4. Die Abbildung von Martin Sundermann zeigt die Dynamik eines Quantenzustandes, der an einer eindimensionalen Potentialschwelle gestreut wird,
siehe Übung 9. Die horizontale Achse zeigt die Zeit, die vertikale den Ort, die Falschfarbendarstellung gibt das Betragsquadrat der Wellenfunktion an.