Dozent: Johannes Berg
Übungen: Nico Riedel

Diese Vorlesung gibt eine Einführung in mathematische Methoden, derer sich die Physik (und viele weitere Wissenschaften) zur Beschreibung der Natur bedient. Themen sind

1. Vektorräume Begriffe und Beispiele, Linearformen und der Dualraum, lineare Abbildungen, Koordinatensysteme und -transformationen, Hauptachsentransformation
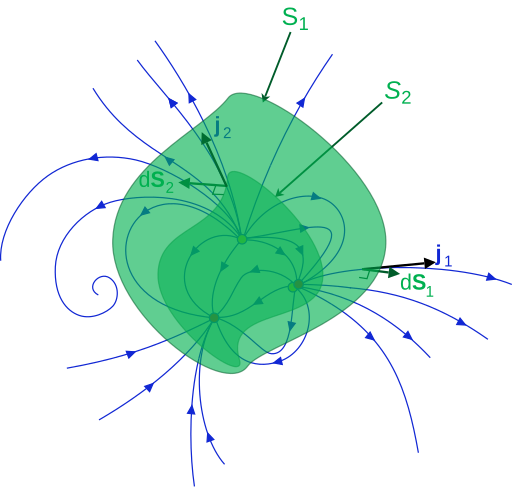
2. Vektoranalysis Vektorfelder und 1-Formen, Differential, Gradient, Rotation, Divergenz, Linien-, Flächen-, und Volumenintegral, krummlinige Koordinaten, Satz von Stokes
3. Potenzreihen Konvergenz; Taylorreihen
    Komplexe Zahlen und Funktionen Eulersche Formel; komplexer Logarithmus
4. Differentialgleichungen Existenz und Eindeutigkeit der Lösung, Schwingungen und die Wellengleichung
5. Fouriertransformation, Distributionen, Greenfunktionen

Zusätzlich zu Vorlesung und Übungen bieten wir eine Fragestunde an, in der Sie Fragen zum Vorlesungsstoff stellen können. Die Fachschaft der Physik bietet ausserdem noch Tutorien zu dieser Vorlesung; Details sind hier zu finden.

Kenntnisse in Linearer Algebra und Integral- und Differentialrechnung werden vorausgesetzt. Der Besuch des Vorkurses wird daher wärmstens empfohlen.

Vorlesungen: Montag 12:00-13:30 in Hörsaal II und Mittwoch 14:00-15:30 ebenso in Hörsaal II, erste Vorlesung ist am 2. April
Übungen: finden Mittwochs und Donnerstags in Kleingruppen statt. Die Anmeldung zu den Übungen erfolgt online.
Die genauen Einteilung in Gruppen finden Sie dann auf der Übungsseite, ebenso die einzelnen Übungen. Die Abgabe der Übungen ist in der Vorlesung am Montag.
Die erste Übung findet dann am Mittwoch/Donnerstag den 18. und 19. 4. statt.
Fragestunde: Donnerstags 10:00-11:30 im Seminarraum des Instituts für Kernphysik (Achtung, im Vorlesungsverzeichnis ist ein falscher Ort angegeben)
Klausur: Dienstag 24.7.2012, 10:00, Hörsaal I+II, Dauer ca. 3h
Nachklausur: 4.10.2012, 14:30, HS I

Die Klausurergebnisse sind hier. Aus der angegebenen Punktzahl (aus 100 erreichbaren Punkten) ergibt sich die Note wie folgt: >=90 1.0; 85-89.5 1.3; 81-84.5 1.7; 76-80.5 2.0; 72-75.5 2.3; 68-71.5 2.7; 64-67.5 3.0; 59-63.5 3.3; 54-58.5 3.7; 50-53.5 4;<50 nicht bestanden.Ein Termin zur Klausureinsicht wird in den nächsten Wochen auf der Übungsseite bekannt gegeben.

Einführend

Großmann, Mathematischer Einführungskurs für die Physik (Teubner)

Begleitend

Arens, Hettlich, Karpfinger, Kockelkorn, Mathematik (Spektrum)
Lang und Pucker, Mathematische Methoden in der Physik (Spektrum)
Fischer und Kaul, Mathematik für Physiker (Teubner)
Berendt und Weimar, Mathematik für Physiker (Physik Verlag)
Jänich, Mathematik - geschrieben für Physiker (Springer)

Weiterführend

Kerner und von Wahl, Mathematik für Physiker (Springer)

Scheinkriterium ist für Bachelor-Studierende das Bestehen der Klausur zum Ende des Semesters. Die Zulassung zur Klausur erfordert regelmäßige und erfolgreiche Teilnahme an den Übungen und das Erreichen von mindestens der Hälfte der Übungspunkte.

Die Vorlesung ist Teil der Pflichtveranstaltungen des Bachelor in Physik.