Genomic sequences and biomolecules
Sequence alignment is the most widely used data analysis tool in molecular biology. Detecting and quantifying sequence similarities is an intricate statistical problem, which has profound connections to the statistical physics of systems with quenched disorder. Other projects in this area are concerned with long-range correlations in genomes and with the statistics of RNA secondary structures.
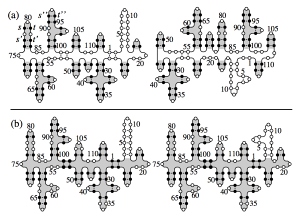
The secondary structure of a random RNA molecule is frozen at low temperatures (a) and molten at higher temperatures (b).
Freezing of random RNA
M. Lässig and K. Wiese, Phys. Rev. Lett. 96, 228101, (2006)
We study secondary structures of random RNA molecules by means of a renormalized field theory based on an expansion in the sequence disorder. We show that there is a continuous phase transition from a molten phase at higher temperatures to a low-temperature glass phase. The primary freezing occurs above the critical temperature, with local islands of stable folds forming within the molten phase. The size of these islands defines the correlation length of the transition. Our results include critical exponents at the transition and in the glass phase.
Universality of log-range correlations in expansion-randomization systems
P.W. Messer, M. Lässig, and P.F. Arndt, J. Stat. Mech., P10004, (2005)
We study the stochastic dynamics of sequences evolving by single site mutations, segmental duplications, deletions, and random insertions. These
processes are relevant for the evolution of genomic DNA. They define a universality class of non-equilibrium 1D expansion–randomization systems with generic stationary long-range correlations in a regime of growing sequence length. We obtain explicitly the two-point correlation function of the sequence composition and the distribution function of the composition bias in sequences of finite length. The characteristic exponent χ of these quantities is determined by the ratio of two effective rates, which are explicitly calculated for several specific sequence evolution dynamics of the universality class. Depending on the value of χ, we find two different scaling regimes, which are distinguished by the detectability of the initial composition bias. All analytic results are accurately verified by numerical simulations. We also discuss the non-stationary build-up and decay of correlations, as well as more complex evolutionary scenarios, where the rates of the processes vary in time. Our findings provide a possible example for the emergence of universality in molecular biology.
Solvable sequence evolution models and genomic correlations
P.W. Messer, P.F. Arndt, and M. Lässig, Phys. Rev. Lett. 94, 138103, (2005)
We study a minimal model for genome evolution whose elementary processes are single site mutation, duplication and deletion of sequence regions, and insertion of random segments. These processes are found to generate long-range correlations in the composition of letters as long as the sequence length is growing; i.e., the combined rates of duplications and insertions are higher than the deletion rate. For constant sequence length, on the other hand, all initial correlations decay exponentially. These results are obtained analytically and by simulations. They are compared with the long-range correlations observed in genomic DNA, and the implications for genome evolution are discussed.
Toward an accurate statistics of gapped alignments
M. Kschischo, M. Lässig, and Y.-K. Yu, Bull. Math. Biol. 67, 169, (2005)
Sequence alignment has been an invaluable tool for finding homologous sequences. The significance of the homology found is often quantified statistically by p-values. Theory for computing p-values exists for gapless alignments [Karlin and Altschul 1990, Karlin and Dembo A 1992], but a full generalization to alignments with gaps is not yet complete. We present a unified statistical analysis of two common sequence comparison algorithms: maximum-score (Smith-Waterman) alignments and their generalized probabilistic counterparts, including maximum-likelihood alignments and hidden Markov models. The most important statistical characteristic of these algorithms is the distribution function of the maximum score S
max, resp. the maximum free energy F
max, for mutually uncorrelated random sequences. This distribution is known empirically to be of the Gumbel form with an exponential tail P(S
max > x) approximately exp(-λx) for maximum-score alignment and P(F
max > x) approximately exp(-λx) for some classes of probabilistic alignment. We derive an exact expression for lambda for particular probabilistic alignments. This result is then used to obtain accurate lambda values for generic probabilistic and maximum-score alignments. Although the result demonstrated uses a simple match-mismatch scoring system, it is expected to be a good starting point for more general scoring functions.
Evolutionary games and quasispecies
F. Tria, M. Lässig, L. Peliti, Europhys. Lett. 62, 446 (2003)
We discuss a population of sequences subject to mutations and frequency- dependent selection, where the fitness of a sequence depends on the composition of the entire population. This type of dynamics is crucial to understand, for example, the coupled evolution of different strands in a viral population. Mathematically, it takes the form of a reaction- diffusion problem that is nonlinear in the population state. In our model system, the fitness is determined by a simple mathematical game, the hawk-dove game. The stationary population distribution is found to be a quasispecies with properties different from those which hold in fixed fitness landscapes.
Scaling laws and similarity detection in sequence alignment with gaps
D. Drasdo, T. Hwa, and M. Lässig, J. Comput. Biol. 7, 115, (2000)
We study the problem of similarity detection by sequence alignment with gaps, using a recently established theoretical framework based on the morphology of alignment paths. Alignments of sequences without mutual correlations are found to have scale-invariant statistics. This is the basis for a scaling theory of alignments of correlated sequences. Using a simple Markov model of evolution, we generate sequences with well-defined mutual correlations and quantify the fidelity of an alignment in an unambiguous way. The scaling theory predicts the dependence of the fidelity on the alignment parameters and on the statistical evolution parameters characterizing the sequence correlations. Specific criteria for the optimal choice of alignment parameters emerge from this theory. The results are verified by extensive numerical simulations.
Finite-temperature sequence alignment
M. Kschischo and M. Lässig, Pacific Symposium on Biocomputing 5, (2000) (refereed)
We develop a statistical theory of probabilistic sequence alignments derived from a 'thermodynamic' partition function at finite temperature. Such alignments are a generalization of those obtained from information-theoretic approaches. Finite-temperature statistics can be used to characterize the significance of an alignment and the reliability of its single element pairs.
Optimal detection of sequence similarity by local alignment
T. Hwa and M. Lässig, Proceedings of the second annual conference on computational molecular biology (RECOMB 98), ACM Press, New York (1998) (refereed)
The statistical properties of local alignment algorithms with gaps are analyzed theoretically for uncorrelated and correlated random sequences. In the vicinity of the log-linear phase transition, the statistics of alignment with gaps is shown to be characteristically different from that of gapless alignment. The optimal scores obtained for uncorrelated sequences obey certain robust scaling laws. Deviation from these scaling laws signals sequence homology, and can be used to guide the empirical selection of scoring parameters for the optimal detection of sequence similarities. This can be accomplished in a computationally efficient way by using a novel approach focusing on the score profiles. Furthermore, by assuming a few gross features characterizing the statistics of underlying sequence-sequence correlations, quantitative criteria are obtained for the choice of optimal scoring parameters: Optimal similarity detection is most likely to occur in a region close to the log side of the loglinear phase transition.
Similarity detection and localization
T. Hwa and M. Lässig, Phys. Rev. Lett. 76, 2591, (1996)
The detection of similarities between long DNA and protein sequences is studied using concepts of statistical physics. It is shown that mutual similarities can be detected by sequence alignment methods only if their amount exceeds a threshold value. The onset of detection is a critical phase transition viewed as a localization-delocalization transition. The fidelity of the alignment is the order parameter of that transition; it leads to criteria to select optimal alignment parameters.
go back 


