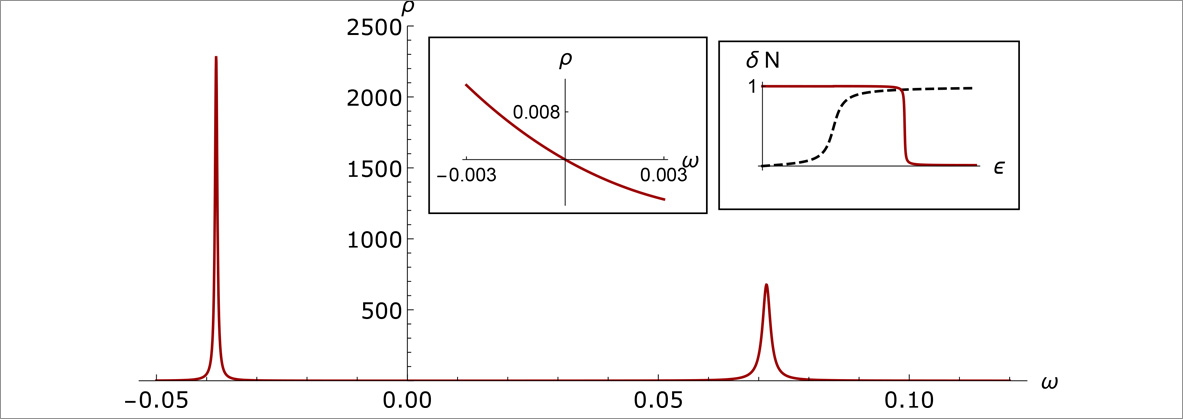
Quantum chaos and disorder:
The majority of physical systems encountered in daily life are partially, sometimes even fully chaotic. The same principle applies in the quantum world where chaos may be induced by fabrication imperfections in quantum devices, impurities in condensed matter systems, or the chaotic dynamics of black holes. Quantum disorder and chaos generate a multitude of phenomena including strong quantum fluctuations in observables, single and many particle quantum localization, and various types of unique quantum phase transitions. They are a source of fluctuations as much as of simplicity and universality. In chaotic dynamics microscopic details are ‘washed out’ which makes universal signatures such as dimensionality, symmetries, or topology stand out more clearly. This principle reflects in beautiful quantum field theories describing matter in the presence of chaos and disorder.
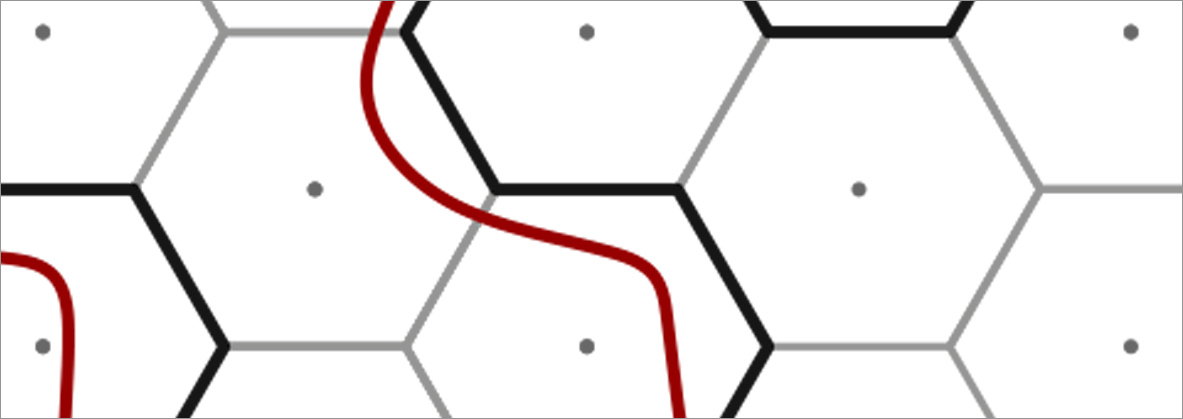
Disordered topological quantum matter:
The physics of topological phases of matter has become one of the most exciting fields of modern physics. Our group explores the properties of topological quantum matter under the real life condition that translational invariance is broken by material imperfections and disorder. How can we understand the robustness of topology in disordered systems? Topological invariants are routinely computed with reference to crystal momenta — how do we describe them if translational invariance is absent and crystal momenta are no longer defined? And how do we understand the physics of topological phase transitions driven by disorder? These are examples of questions are central to our recent work in the field.
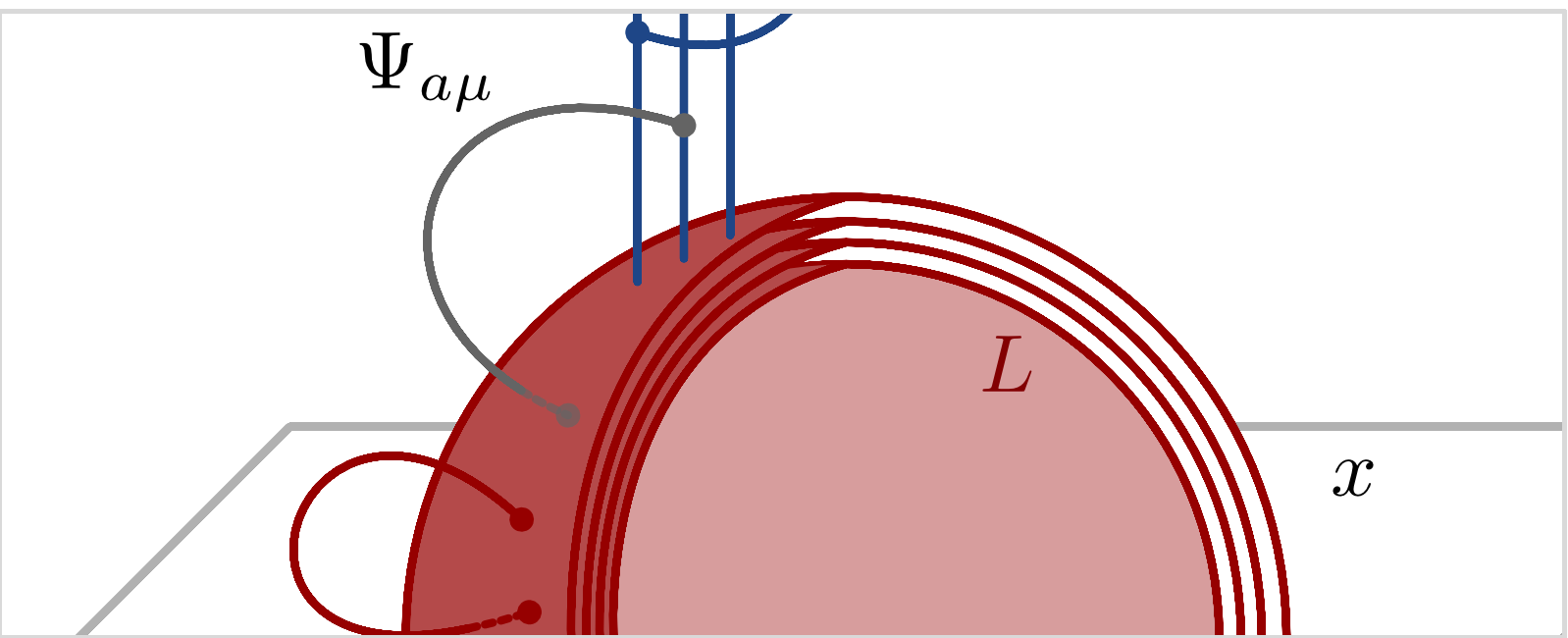
Quantum chaos in gravity:
Spectra and wave functions of quantum chaotic systems show universal correlations which have been described in terms of a multitude of concepts, including random matrix theory, diagrammatic perturbation theory, or quantum field theory. While most of these were developed in fields such as condensed matter or many body physics, more recent work aims to extend the concept of quantum chaotic universality to gravity. These ideas assume their most concrete form in the construction of a low-dimensional holographic correspondences, and the observation of chaotic correlations in gravitational path integrals. Contributing expertise in field theoretical approaches to quantum chaos, our group is increaingly active in this line of research.