Verkehrsmodelle

[english version]

Zellularautomaten sind Modelle, die diskret in der Zeit, im Raum und in der Zustandsvariablen sind. Letzteres unterscheidet sie z.B. von diskretisierten Differentialgleichungen. Auf Grund der Diskretheit erlauben Zellularautomaten eine äusserst effiziente Implementierung für Computersimulationen.

Zur Beschreibung des Zustandes einer Strasse mit Hilfe eines Zellularautomaten unterteilt man diese zunächst in Zellen der Länge 7.5 m. Dies entspricht dem Platzbedarf (Fahrzeuglänge + Abstand zum Vordermann) eines Autos in einem dichten Stau. Jede Zelle kann nun leer oder durch genau ein Auto besetzt sein. Die Fahrzeuge werden durch ihre momentane Geschwindigkeit v charakterisiert, die die Werte v=0,1,2,... ,v_max annehmen kann. v_max entspricht dabei z.B. einer Geschwindigkeitsbeschränkung und ist deshalb im einfachsten Falle für alle Fahrzeuge gleich. Eine typische Konfiguration zeigt die folgende Abbildung.

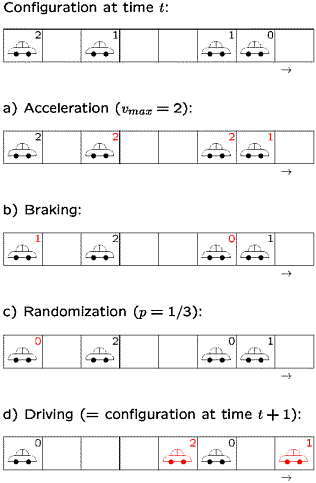
Als Nächstes benötigt man Regeln, die die zeitliche Entwicklung eines gegebenen Zustandes definieren. Der einfachste Regelsatz, der zu einem realistischen Verhalten führt, wurde 1992 von Nagel und Schreckenberg [3] angegeben. Er besteht aus 4 Schritten, die jeweils auf alle Fahrzeuge gleichzeitig anzuwenden sind (parallele Dynamik).

Schritt 1: Beschleunigung Alle Fahrzeuge, die noch nicht die Maximalgeschwindigkeit vmax erreicht haben, beschleunigen um eine Einheit: v -> v+1 Schritt 2: Sicherheitsabstand Sieht ein Fahrzeug d freie Zellen vor sich und ist seine Geschwindigkeit v (nach Schritt 1) grösser als d, so wird die Geschwindigkeit auf d reduziert: v -> min{d,v} Schritt 3: Trödeln Die Geschwindigkeit wird zufällig mit der Wahrscheinlichkeit p um eine Einheit vermindert (wenn nach Schritt 2 v>0 war): v -> v-1 Schritt 4: Fahren Nachdem in den Schritten 1-3 die neue Geschwindigkeit vn für jedes Fahrzeug n bestimmt wurde, bewegt sich dieses nun um vn Zellen vorwärts: xn -> xn+vn. Die rechtseitige Abbildung zeigt an einem Beispiel, wie sich die Konfiguration zur Zeit t+1 durch schrittweises Anwenden der Regeln aus der Konfiguration zur Zeit t ergibt.

Was bedeuten diese Regeln? Schritt 1 beschreibt z.B. den Wunsch der Fahrer, so schnell wie möglich bzw. erlaubt zu fahren. Schritt 2 beinhaltet die Wechselwirkung zwischen den Fahrzeugen und dient der Vermeidung von Unfällen. Schritt 3 erfasst auf ganz einfache Art und Weise eine ganze Reihe von Effekten, die im realen Verkehr eine wichtige Rolle spielen. So wird ein einzelnes Fahrzeug niemals konstant mit exakt der gleichen Geschwindigkeit fahren, sondern die Reisegeschwindigkeit wird leicht fluktuieren. Ein ganz wichtiger Punkt sind die überreaktionen beim Bremsen. Ein Fahrzeug, das z.B. in Schritt 2 etwas abbremsen musste, wird mit der Wahrscheinlichkeit p noch weiter abbremsen, als es eigentlich nötig wäre. Dies kann zu einer Kettenreaktion führen, wenn die Fahrzeugdichte gross genung ist. Schliesslich kommt ein Fahrzeug zum Stehen und löst einen Stau aus. Dieser ist ohne offensichtlichen äusseren Anlass entstanden und wird deshalb als ``Stau aus dem Nichts'' oder spontaner Stau bezeichnet. Hier zeigt sich ganz deutlich die wichtige Bedeutung von Schritt 3, der das nicht perfekte Verhalten der Autofahrer widerspiegelt. In Schritt 4 werden schliesslich die Fahrzeuge gemäss ihrer neuen Geschwindigkeit weiterbewegt.

Der obige Regelsatz ist minimal in dem Sinne, dass man bei Weglassen einer der Regeln kein realistisches Verhalten mehr findet. Unter realistischem Verhalten verstehen wir hier das Auftreten spontaner Staus und die richtige Form des sogenannten Fundamentaldiagramms, d.h. des Zusammenhangs zwischen Dichte und Fahrzeugstrom. Für kleine Dichten ist der Strom proportional zur Dichte, da die Autos fast nicht miteinander wechselwirken und somit mit ihrer Wunschgeschwindigkeit v_max (bis auf Fluktuationen durch den Trödelschritt) fahren. Bei höheren Dichten wird die Wechselwirkung wichtig und man findet Abweichungen vom linearen Verhalten. Schliesslich dominiert die Wechselwirkung sogar und der Strom nimmt mit steigender Dichte wieder ab.

Die Dynamik lässt sich sehr gut mit Hilfe eines Java-Applets verfolgen. Links unten sieht man die Darstellung der Fahrzeugpositionen auf dem Ring (periodische Randbedingungen, die Autos fahren ``im Kreis''). Das Fenster darüber zeigt die Trajektorien der einzelnen Fahrzeuge. Der linke Rand (blaue Linie) entspricht dabei dem blauen Strich (bei 3 Uhr) in der Darstellung links unten. Die Fahrzeuggeschwindigkeiten werden durch unterschiedliche Farben gekennzeichnet. Die augenblickliche Geschwindigkeitsverteilung wird unten in der Mitte dargestellt. Daneben findet man die momentane Verteilung der Abstände zum Vordermann (gaps). Die drei Diagramme rechts neben der Darstellung der Fahrzeugtrajektorien sind verschiedene Formen des Fundamentaldiagramms. Im obersten Diagramm wird der Strom als Funktion der Dichte dargestellt. Dies ist die klassische Form des Fundamentaldiagramms. Darunter findet man die Durchschnittsgeschwindigkeit als Funktion der Dichte bzw. als Funktion des Stromes. Alle drei Darstellungen sind aber äquivalent, da die drei Grössen Dichte r, Strom J und Durchschnittsgeschwindigkeit v nicht unabhängig voneinander sind, sondern über J=r v zusammenhängen. Es sei hier bemerkt, dass die Messgrössen, die in den Fundamentaldiagrammen dargestellt werden, lokal gemessen werden, d.h. es wird jeweils nur über einen Teilbereich des Ringes gemittelt. Deshalb ist es möglich, dass die (lokale) Dichte verschiedene Werte annehmen kann, obwohl die Gesamtzahl der Fahrzeuge (und damit die globale Dichte) festgehalten wird.

In der Simulation erkennt man deutlich die auftretenden spontanen Staus (rot). Man sieht auch das typische stop-and-go Verhalten, bei dem man kurz nach dem Verlassen eines Staus bereits in den nächsten gerät. Wenn man die globale Dichte mit Hilfe des Schiebereglers ``global density'' verändert, sieht man deutlich, wie sich die Zahl der auftretenden Staus ändert. Interessant ist es auch, den Trödelparameter p über ``Slowdown prob. p'' bei fester Dichte zu verändern. Man beachte insbesondere, das man für p=0 ein ganz anderes Verhalten erhält.

Mit dem Applet lässt sich auch eine interessante Variante des Nagel-Schreckenberg Modells simulieren. Dazu klicke man auf den Button ``NaSch'' über den Trajektorien und wähle ``VDR'' aus. VDR ist die Abkürzung von ``velocity-dependent randomization'' und bezeichnet den entscheidenden Unterschied zum NaSch Modell. In letzterem ist der Trödelparameter p konstant. Im VDR-Modell [4] hingegen, hängt p von der Geschwindigkeit des Fahrzeuges nach dem letzten Zeitschritt ab. Für stehende Fahrzeuge wählt man für den Trödelparameter einen höheren Wert p₂ als den Wert p für fahrende Fahrzeuge. Das VDR-Modell unterscheidet sich daher vom NaSch-Modell nur durch den neuen

Schritt 0: Bestimmung des Trödelparameters p(v) Für stehende Fahrzeuge (v=0) ist p(v=0)=p2. Für fahrende Fahrzeuge (v>0) ist p(v)=p,

der vor den anderen Schritten auszführen ist. Alle anderen Schritte bleiben unverändert. p₂ lässt sich über den Regler ``Slowdown prob. of stopped cars p2'' steuern.

Um den Unterschied im Verhalten von NaSch-Modell und VDR-Modell deutlich zu sehen, wähle man ein relativ kleines p, z.B. p=0.01 und ein relativ grosses p₂, z.B. p₂=0.5. Man sieht deutlich, dass sich (für nicht zu kleine Dichten) nach einiger Zeit ein phasenseparierter Zustand herausbildet, der aus einem grossen kompakten Stau und einem staufreien Freiflussbereich besteht.

Literatur:

[1]	D. Chowdhury, L. Santen and A. Schadschneider: Statistical physics of vehicular traffic and some related systems , Physics Reports 329, 199 (2000)
[2]	S. Wolfram, Theory and Applications of Cellular Automata, (World Scientific, 1986)
[3]	K. Nagel and M. Schreckenberg, A cellular automaton model for freeway traffic, J. Physique I 2, 2221 (1992)
[4]	R. Barlovic, L. Santen, A. Schadschneider and M. Schreckenberg, Metastable states in cellular automata for traffic flow, Eur. Phys. J. B 5, 793 (1998)