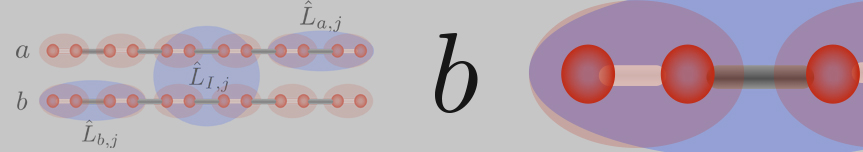RESEARCH INTERESTS
Quantum information science is a highly interdisciplinary field that spans a wide array of both fundamental and applied topics in physics, mathematics, computer science and engineering. Our research group focuses on various problems in theoretical quantum information science, with a focus on applications to many body physics.
Here are brief summaries of some of the research topics.
Machine learning and computational physics
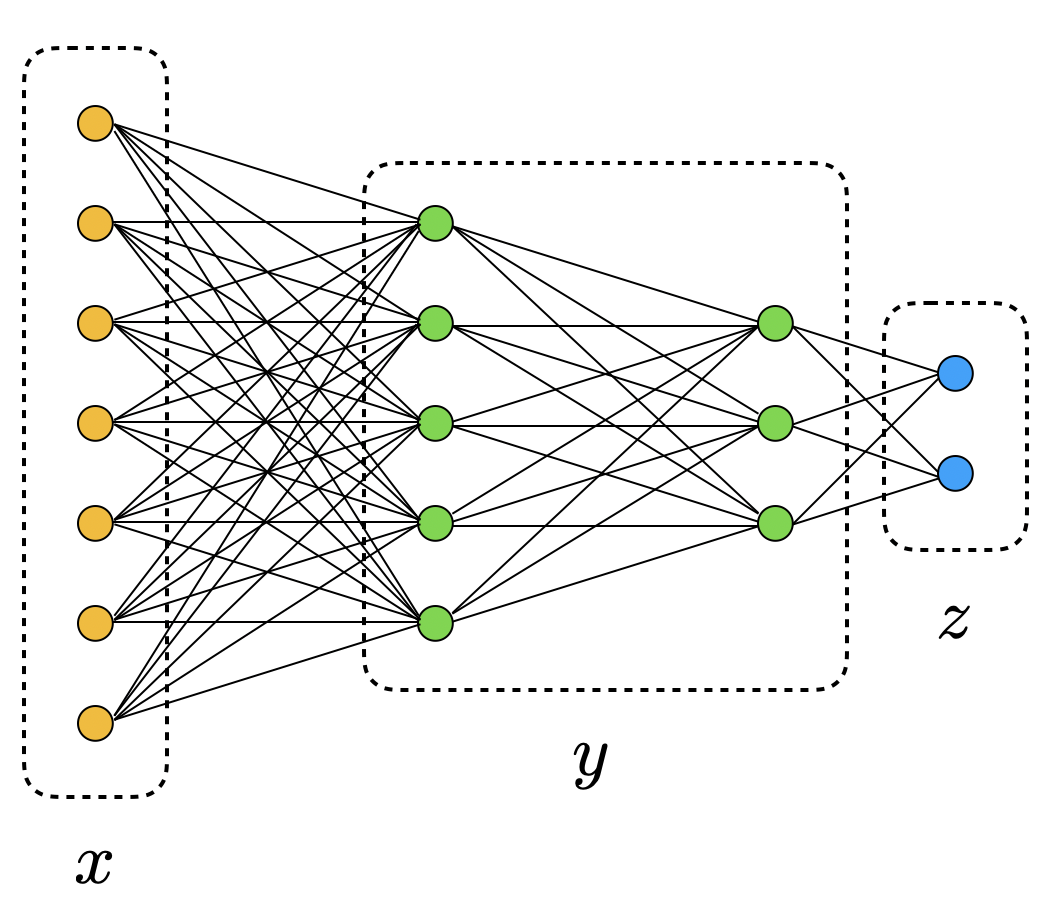
At present, most of the work in are group is devoted to problems lying at the intersection of machine learning, practical quantum computing (including quantum chemistry) and computational physics. Variational optimization methods have played and important role in the development of physics for a long time already. Recently these methods have seen a renewal of interest due on the one hand to the recent advances in machine learning, and on the other to the newly accessible cloud quantum computing. Our research group is working actively on these topics trying to answer a number of fundamental questions:
- Can tools from machine learning lead to improvements in quantum Monte Carlo methods, including ground state energy estimation.
- How powerful are 'positive' wavefunctions for quantum computation and quantum optimization?
- What are good classes of Ansatz states for Quantum Variational Eigensolvers (QVE)? What problems are well suited for QVE on near-term quantum computers? Are there any classical optimization problems that can be solved more efficiently on a near term quantum computer?
- Can methods from many body physics and quantum information theory teach us something (rigorous) about the efficiency and/or generalization ability of (deep) learning algorithms?
Tensor Networks and many body correlations.
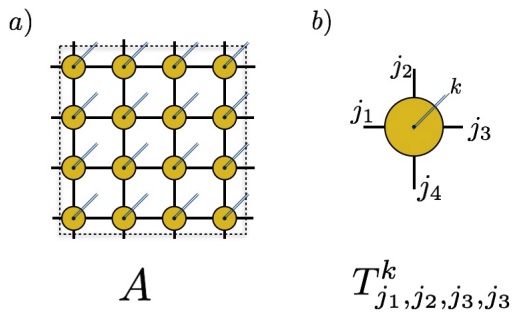
Most quantum states are not nearly as entangled as one might naively expect. In particular, states that are generated by local dynamics, or that are the ground states of local hamiltonians will typically have entanglement the scales with the area of a region rather than the volume. The group has worked on a number of problems relating to tensor networks representations of quantum many body states. Our focus has mostly been on characterizing how efficiently certain classes of states can be prepared on a classical or quantum computer, and what types of correlations are allowed in such systems. An important breakthrough has been the to connect properties of the boundary of a tensor network state to properties of the bulk, In particular, together with collaborators, we showed that the bulk system is gapped is the boundary state is of approximate Gibbs form. We are still working on proving bulk gap for specific models, such as the AKLT model. Lattice analysis of the conditional mutual information plays a very important role in these studies.
Quantum error correction
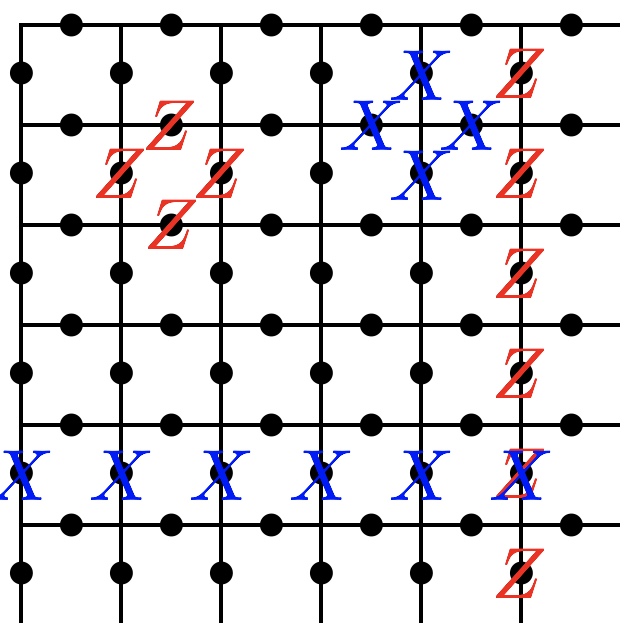
Quantum systems are resolutey faulty in a manner that has no analogue in the macroscopic world of classical physics. This would appear to exclude the possibility of arbitrarily long and precise quantum computation. Fortunately one of the early insights of the quantum computing pioneers was that quantum error correction could be used to perform arbitrarily precise and long quantum computation at the cost of (potentially) severe resource overhead. Since then the field of quantum error correction has been working towards the design and analysis of strategies for encoding and processing quantum information at arbitrary precision with the fewest number of physical qubits, and the most amenable geometrical architectures. Connections between statistical mechanics and decoding have been our main focus recently.