Research
The group's work sits at the intersection of statistical mechanics and quantitative biology. Central to this is the relationship between fluctuations and noise in biological systems, the corresponding statistical ensembles, and biological function. This connection manifests itself across various levels and timescales, from stochastic modeling of gene expression to the evolution of regulatory DNA. Our current research focuses on tumour evolution and the emergence of resistance to cancer therapy.
Tumour evolution
|
|
Mutations in tumours can serve as markers for tracking their evolutionary history. In collaboration with the Weghorn Lab (Barcelona), we investigated the spatio-temporal dynamics of early-stage tumours. Using published data from resected hepatocellular carcinomas, which included several hundred samples taken in both two and three dimensions, we applied spatial metrics of evolution. Our analysis revealed that tumour cells primarily grew uniformly within the tumour volume, rather than concentrating at its boundary [1].
To further explore tumour evolution, we are currently developing phylodynamic tools for single-cell analysis, grounded in stochastic models of population dynamics during cellular reproduction [2].
|
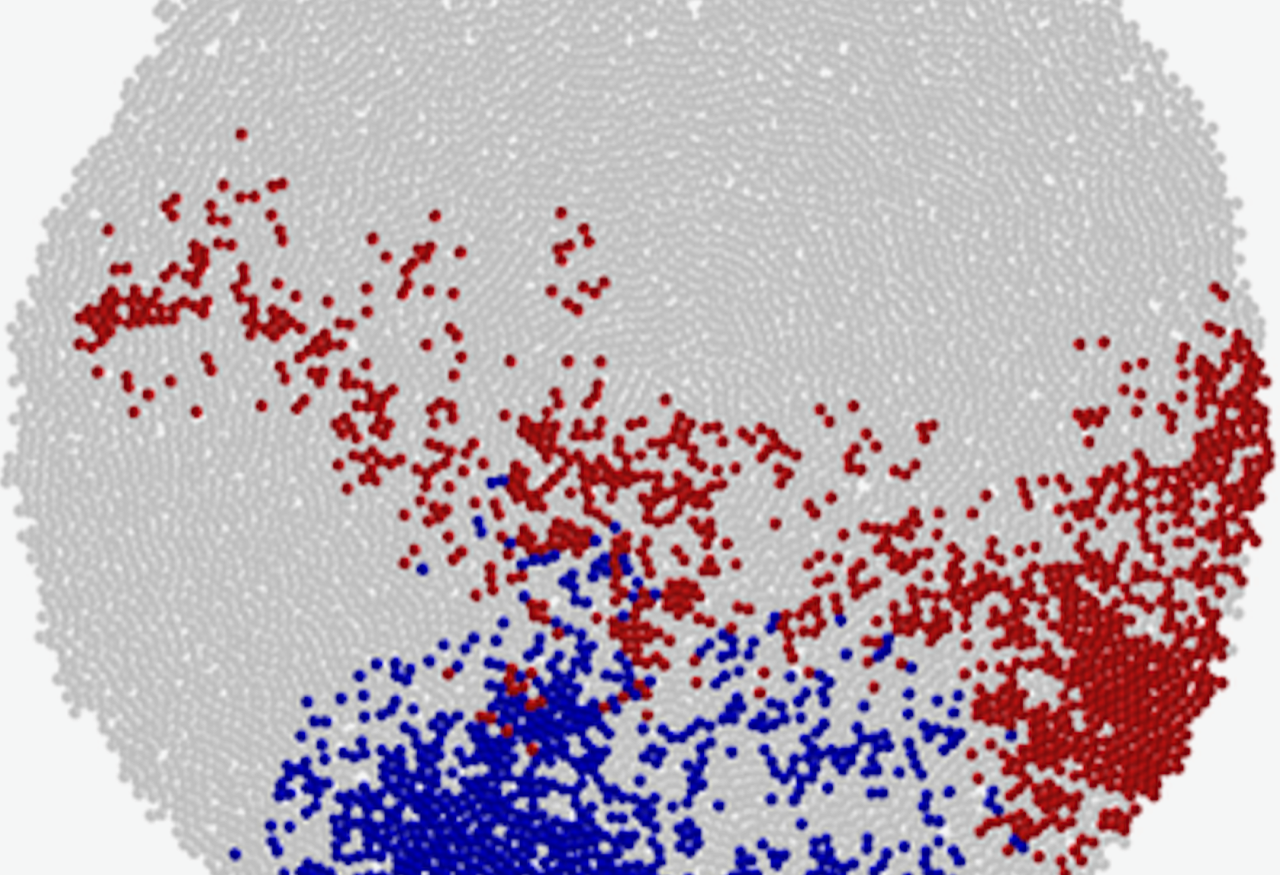
A simulation of population growth demonstrates how cells, by pushing one another aside during expansion, can lead to broad spatial distribution of mutants (cells marked in red). This pattern of mutant dispersion is also observed in empirical tumor data [1].
|
The emergence of resistance to targeted cancer therapy
|
|
Molecularly targeted cancer therapies can lead to rapid tumor regression. However, in most cases, this regression is followed by the swift expansion of therapy-resistant mutants. In collaboration with researchers at the Department of Translational Medicine (Brägelmann and Thomas labs, University Clinic Cologne), we explored the spectrum of mutations conferring resistance to therapy in a cell-line model of lung cancer (PC-9 cells). This work has led to the identification of drug combinations that inhibit all resistant mutants found in a tumor cell population large enough to be detected in a clinical setting. Based on these findings, we are currently investigating dosing strategies tailored to the predicted evolution of resistant clones.
|
Resistant clones emerging in a population of PC-9 cells after 3 weeks of treatment with the EGFR inhibitor erlotinib. In [1], we characterize and target the different resistance mechanisms found in a population corresponding in size to a tumor with a 1 cm diameter.
|
Stochastic dynamics of gene expression
|
|
Gene transcription takes place out of equilibrium, with the rate of expression of a
gene constantly changing due to the presence or absence of specific
proteins called transcription factors. Random fluctuations of
molecular concentrations can have large effects on cells, such as
transitions between metastable states. In a collaboration with
experimentalists of the
Veening lab (EPFL Lausanne), we have pinpointed the fluctuation causing
the transitions between meta-stable states of the paradigmatic lactose-uptake pathway in
E. coli and developed a statistical theory of these
transitions [1,2]. Past work was on
out-of-equilibrium properties of gene expression [3], the determination of
regulatory interactions between genes from gene expression time
series [4], and fluctuations in the dynamics of non-coding RNA [5].
| [1] |
Switching off: the phenotypic transition to the uninduced state of the
lactose uptake pathway,
P. M. Bhogale, R. A. Sorg, J.-W. Veening, and J. Berg,
Biophysical Journal 121(2), 183-192 (2022)
| | [2] |
What makes the lac-pathway switch: identifying the fluctuations that
trigger phenotype switching in gene regulatory systems
P. Bhogale, R. Sorg, J.-W. Veening, J. Berg,
Nucleic Acids Research; doi: 10.1093/nar/gku839 (2014)
| | [3] |
Out-of-equilibrium dynamics of gene expression and the Jarzynski equality,
J. Berg, Phys.Rev.Lett 100, 188101 (2008)
| | [4] |
Dynamics of gene expression and the regulatory inference problem,
J. Berg, Europhys. Lett. 82, 28010 (2008)
| | [5] |
Quantitative analysis of competition in post-transcriptional regulation reveals a novel signature in target expression variation,
F. Klironomos and J. Berg, Biophysical Journal, 104 (4), 951-958 (2013)
|
|
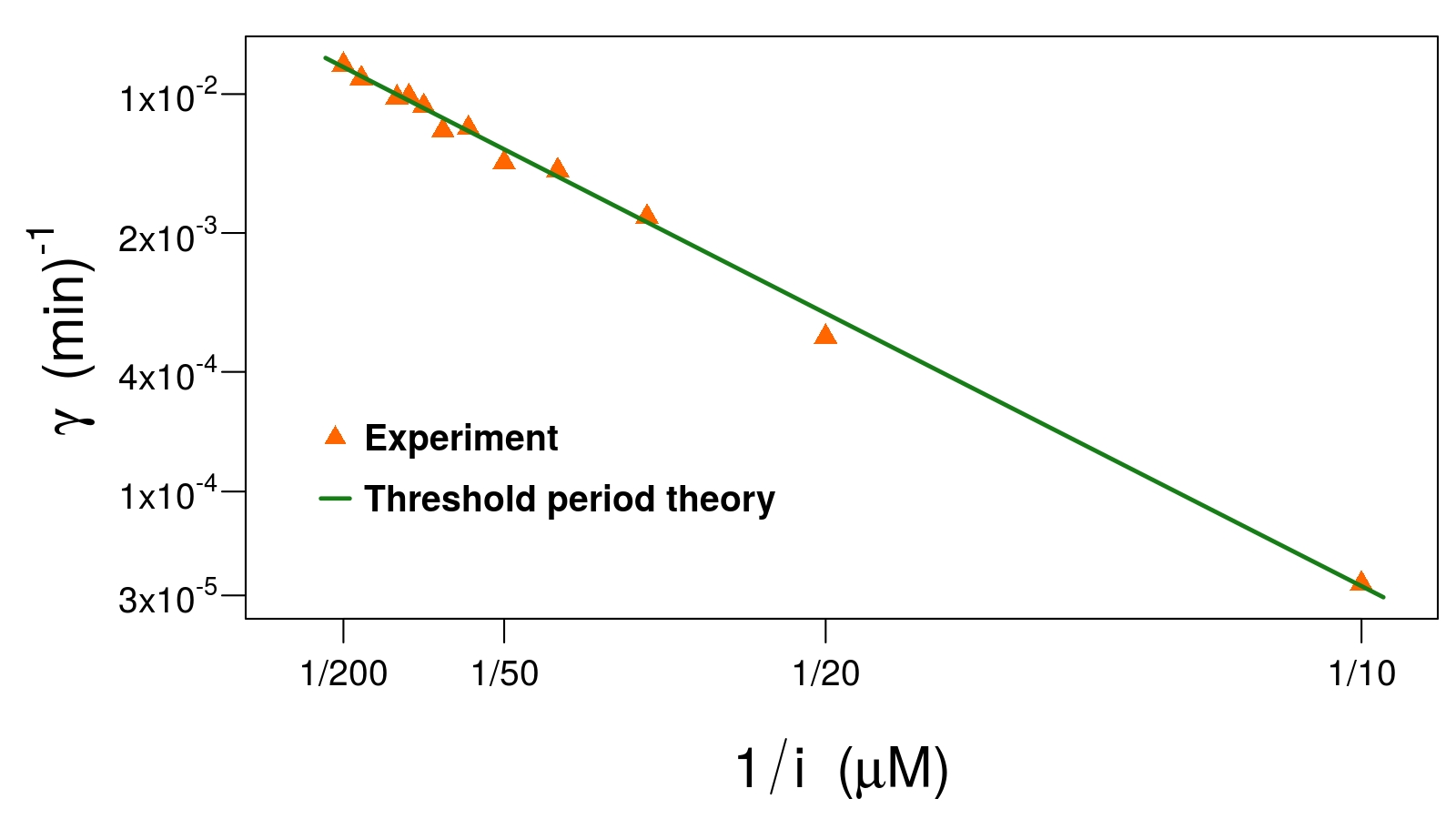The rate at which the lac-pathway switches to the induced state (log-scale)
against the inverse of the inducer concentration. Our model
predicts a simple relationship that is borne out very well
experimentally (orange triangles) [2].
|
Statistical mechanics, inverse problems, and inference
|
|
We study pure and applied problems at the interface between
statistical mechanics and machine learning. An example is the
inverse Ising problem: how to reconstruct couplings and fields of an
Ising model given observables such as spin-spin correlations. We
contributed a novel method based on the Bethe approximation, which is
exact on tree-like lattices [1], and extended mean-field approaches to
both ferromagnetic and glassy low-temperature phases of Ising models [2].
| [1] |
Inverse statistical problems: from the inverse Ising problem to data science,
H.C. Nguyen, R. Zecchina, and J. Berg, Advances
in Physics,
66 (3), 197-261 (2017).
| | [2] |
Mean-field theory for the inverse Ising problem at low temperatures,
H.C. Nguyen and J. Berg, Phys. Rev. Lett. 109, 050602 (2012).
| | [3] |
Bethe-Peierls approximation and the inverse Ising problem,
H.C. Nguyen and J. Berg, J. Stat. Mech., P03004 (2012).
| | [4] |
Significance analysis and statistical mechanics: an application to
clustering,
M. Łuksza, M. Lässig and J. Berg, Phys. Rev. Lett.
105, 220601 (2010).
|
|
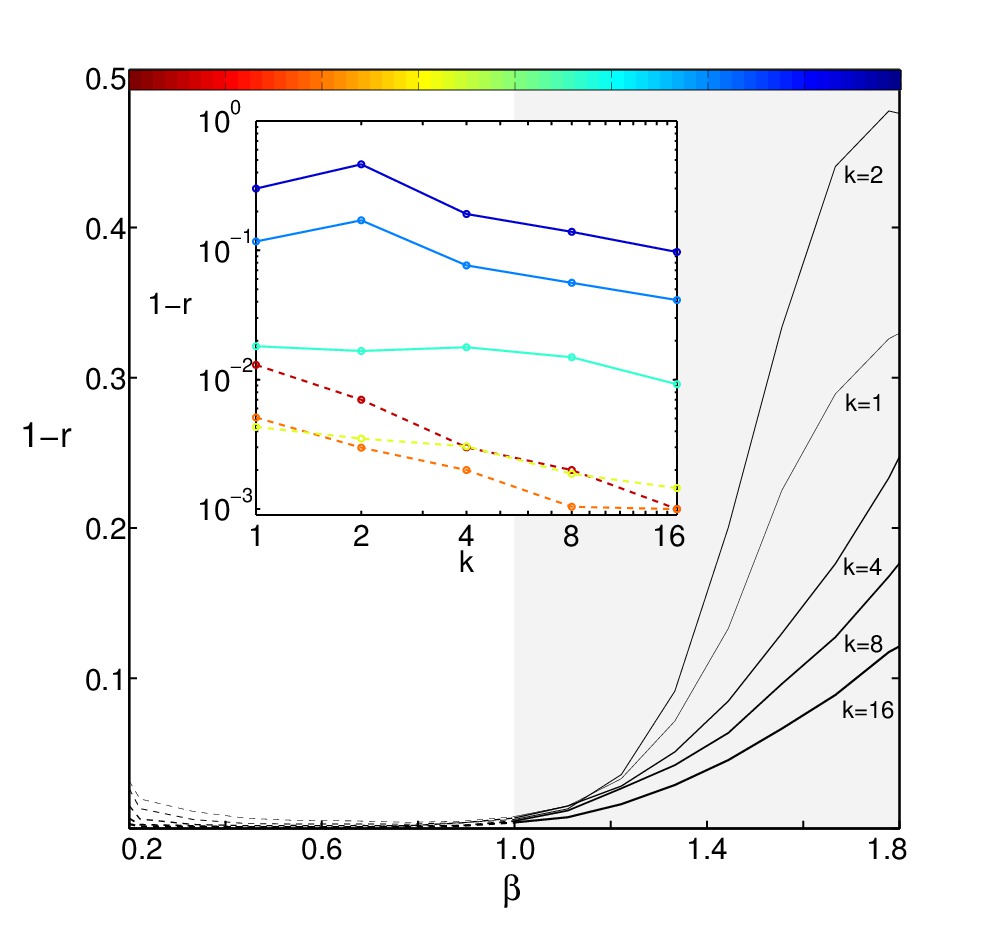Reconstruction error at different temperatures for model with a glassy
low-T phase (SK-model) against inverse temperature and for different
numbers of thermodynamic states. See [2] for details.
|
Back