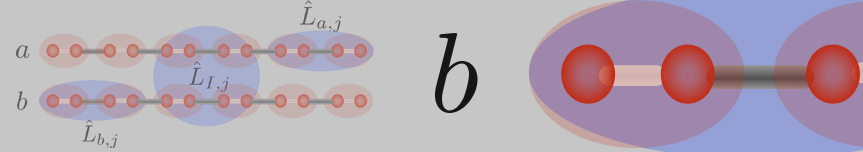RESEARCH INTERESTS
Our research is located on the interface of quantum optics and many-body physics. In quantum optics, traditionally the interaction of light with a few degrees of freedom is considered, such as the energy levels of an atom. The internal atomic dynamics is coherent, but laser drive and coupling to the radiation field gives rise to spontaneous emission and dissipation. On the other hand, typical many-body systems of condensed matter physics involve a continuum of degrees of freedom in space, but most often are not driven externally. However, recently several experimental platforms move into the focus, which combine these aspects. Among them, systems of ultracold atoms in optical cavities, light driven semiconductor heterostructures, microcavity arrays, trapped ions, or Rydberg gases in the dissipative regime.
This creates a novel, genuine non-equilibrium scenario without immediate counterpart in equilibrium condensed matter physics: driven open many-body quantum systems. Their unifying characteristic is the simultaneous appearance of coherent and driven-dissipative quantum dynamics on an equal footing in a macroscopic system. Drive and dissipation violate detailed balance equilibrium conditions strongly on the microscopic level. A prominent goal of our research is to understand how this microscopic driving conditions transforms into macroscopically observable effects: What is the fate of equilibrium phases and phase transitions under such driving conditions? Are there novel non-equilibrium universality classes? Can there be new states of quantum matter emerging from such dynamics? Are drive and dissipation always adversary to fragile quantum mechanical correlations? Is topological order a unique feature of equilibrium ground state systems, or can it also emerge in driven open quantum systems?
In the absence of the usual frameworks for analyzing equilibrium systems, it is necessary to create new theoretical tools to perform the transition from micro- to macrophysics in practice. To this end, one important direction is the development of advanced quantum field theoretical techniques based on the Keldysh field integral. Alternatively, sometimes we can rely on exact solutions. But we also use numerical approaches to foster understanding of such systems.
Here are brief summaries of some of the research topics.
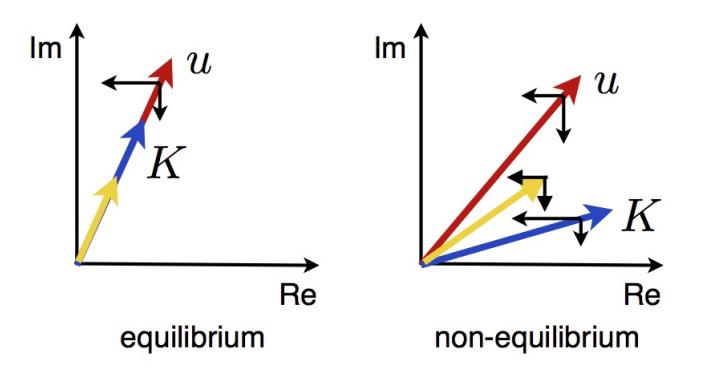
Figure: Schematic RG flow in the complex plain of couplings describing dissipation (Im axis) and coherent (Re axis) dynamics in equilibrium and non-equilibrium. In equilibrium, a dynamical symmetry locks the couplings to a single ray (see "Dynamical Criticality").
Dynamical Criticality
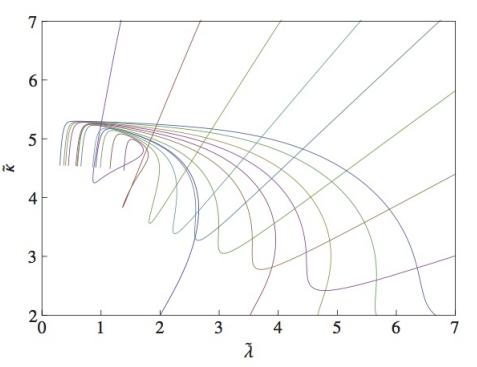
Critical systems show universality: Their long distance correlation functions are governed by power laws characterized by a set of independent critical exponents. These are insensitive to microscopic details and determined by symmetries and dimensionality of the critical system alone. A fundamental question is this: Given the microscopic breaking of detailed balance, is memory on this violation lost by performing the coarse graining to macroscopic distances? Focusing on three dimensions, our analysis shows that, quite surprisingly, this memory is actually partially kept [1]. This is rationalized by the fact that equilibrium and non-equilibrium stationary states are distinct by symmetry [2]. This scenario provides a non-equilibrium analogue of classical dynamical criticality. Going one step further, we investigated an analogue of quantum critical behavior in driven systems. Our results establish a new non-equilibrium quantum universality class not smoothly connected to an equilibrium quantum critical point [3]. Such a scenario is conceivable e.g. in arrays of microcavities coupled to superconducting qubits. To obtain theses results, we have developed a flexible functional renormalization group approach for Keldysh functional integrals. The results were corroborated with alternative field theoretical formulations of the renormalization group, where available [4].
Figure: RG flow from a functional RG approach.
[1] L. Sieberer, S. Huber, E. Altman, S. Diehl, Dynamical critical phenomena in driven-dissipative systems, Phys. Rev. Lett. 110 195301, (2013).
[2] L. M. Sieberer, A. Chiocchetta, A. Gambassi, U. C. Täuber, S. Diehl, Thermodynamic Equilibrium as a Symmetry of the Schwinger-Keldysh Action, Phys. Rev. B 92,134307 (2015).
[3] J. Marino, S. Diehl, Driven Markovian Quantum Criticality, Phys. Rev. Lett. 116, 070407 (2016).
[4] U. Tauber, S. Diehl Perturbative Field-Theoretical Renormalization Group Approach to Driven-Dissipative Bose-Einstein Criticality, Phys. Rev. X 4, 021010, (2014).
Review: L. M. Sieberer, M. Buchhold, S. Diehl, Keldysh Field Theory for Driven Open Quantum Systems, Rep. Prog. Phys. 79, 096001 (2016).
Phase Structure of Driven Open Quantum Systems
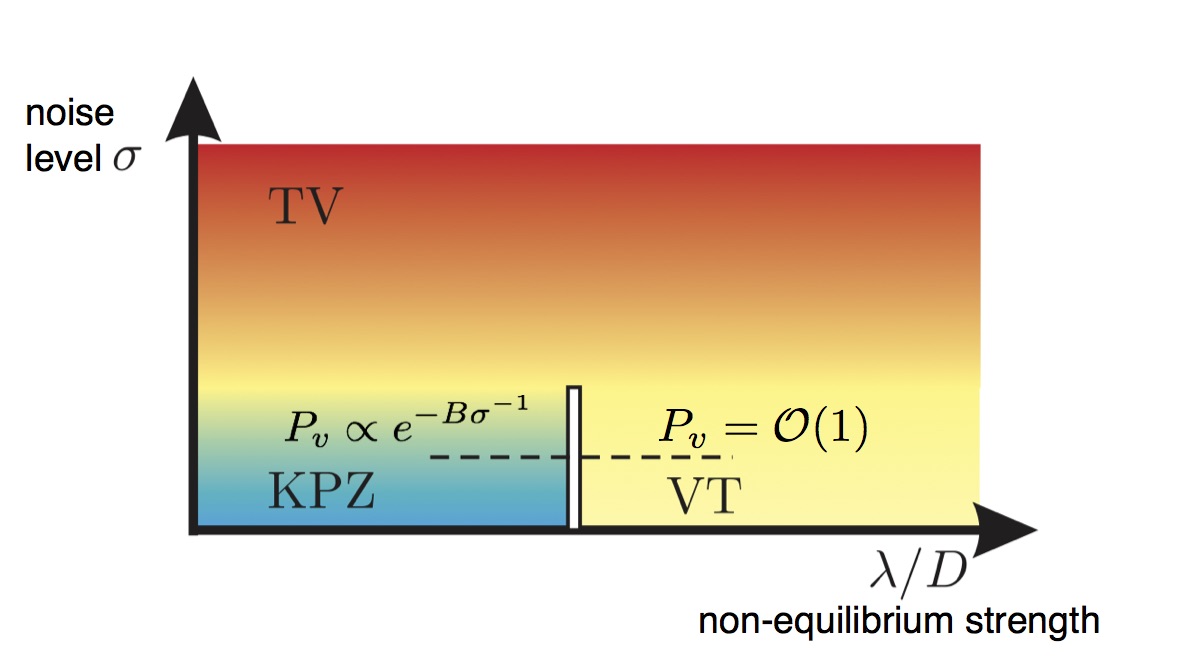
To what extent are the characteristic properties of equilibrium phases robust towards non-equilibrium perturbations? Are there new phases of matter without equilibrium counterpart? Our work shows that specifically low dimensional systems may be very sensitive to non-equilibrium drive. For example, focusing on two dimensions, we found that the characteristic quasi-long range order in low temperature equilibrium systems with continuous symmetries is cut off due to non-equilibrium effects in platforms like exciton-polariton condensates [1]. Strictly speaking, the celebrated Kosterlitz-Thouless transition is absent even for weak non-equilibrium conditions [2,3]. On the other hand, we have established a new first order phase transition into a vortex turbulent state for strong non-equilibrium drive, which does not have an equilibrium analogue [4]. Another platform concerns driven-dissipative Rydberg gases. Here a quantum analogue of directed percolation physics can be realized, resulting in a new absorbing state phase transition [5]. We also studied atoms confined to multimode optical cavities, hosting non-equilibrium spin and photon glasses [6]. All these studies crucially hinge on the development of Keldysh functional integral techniques.
Figure: Non-equilibrium phase diagram of one-dimensional driven open quantum systems (e.g. exciton-polaritons).It exhibits a novel first order phase transition at low noise level as a function of increasing non-equilibrium strength, characterized by a jump in the density of space-time vortices.
[1] E. Altman, L. M. Sieberer, L. Chen, S. Diehl, J. Toner, Two-dimensional superfluidity of exciton-polaritons requires strong anisotropy, Phys. Rev. X 5, 011017 (2015).
[2] L. M. Sieberer, G. Wachtel, E. Altman, S. Diehl, Lattice duality for the compact Kardar-Parisi-Zhang equation, Phys. Rev. B 94, 104521 (2016).
[3] G. Wachtel, L. M. Sieberer, S. Diehl, E. Altman, Electrodynamic duality and vortex unbinding in driven-dissipative condensates, Phys. Rev. B 94, 104520 (2016).
[4] L. He, L. M. Sieberer, S. Diehl, Space-time vortex driven crossover and vortex turbulence in one-dimensional driven open condensates, Phys. Rev. Lett. (2017).
[5] M. Buchhold, B. Everest, M. Marcuzzi, I. Lesanovsky, S. Diehl, Non-equilibrium effective field theory for absorbing state phase transitions in driven open quantum spin systems, Phys. Rev. B 95, 014308 (2017).
[6] M. Buchhold, P. Strack, S. Sachdev, S. Diehl, Dicke-Model Quantum Spin and Photon Glass in Optical Cavities: Non-equilibrium theory and experimental signatures, Phys. Rev. A 87 063622, (2013).
Review: L. M. Sieberer, M. Buchhold, S. Diehl, Keldysh Field Theory for Driven Open Quantum Systems, Rep. Prog. Phys. 79, 096001 (2016).
Order by Dissipation
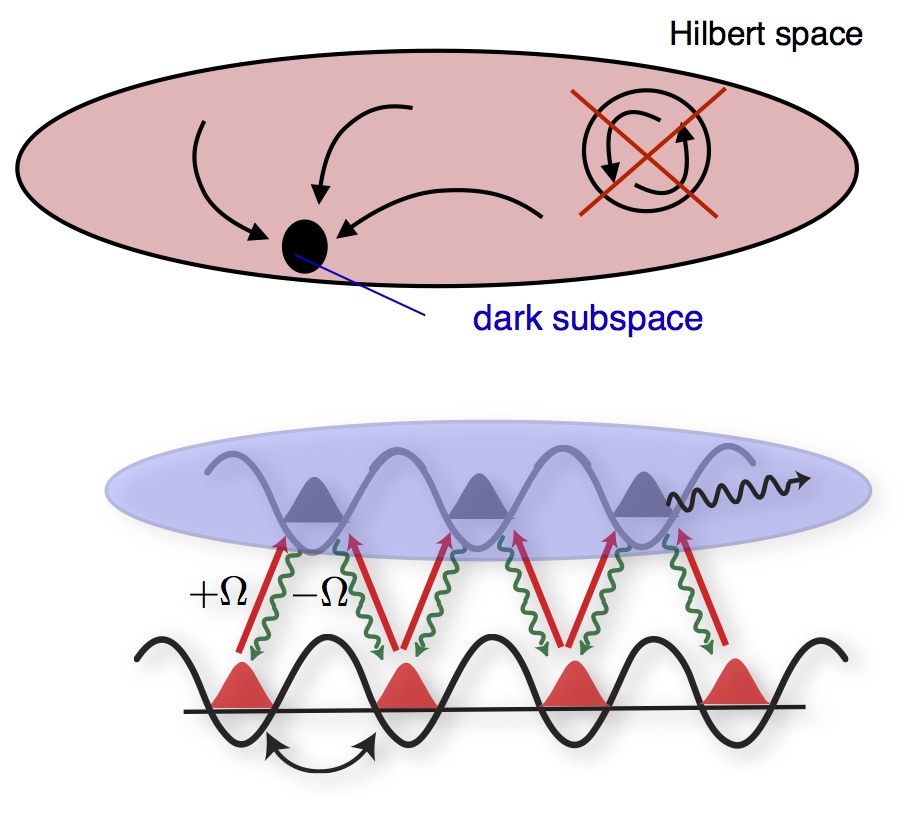
Usually, dissipation acts to degrade the degree of order, and increase the entropy in a physical system. Can this be reversed in a quantum system? The affirmative answer is well known in quantum optics for few degrees of freedom, and underlies, e.g. velocity selective dark state cooling of single atoms. We have leveraged this idea over to many-body systems with exponentially large Hilbert spaces. In this framework, dissipation does not destroy subtle quantum mechanical correlations, but in contrary actually creates them, if drive and dissipation are suitably engineered. This allows us to create quantum mechanical long range order [1], entangled many-body states (see the experiment [2]), and states with topological order of fermions [3]. As a practical perspective, this scheme may be used to cool ultracold fermionic atoms in optical lattices into pure quantum states in a targeted way.
This scenario gives rise to a new arena for many-body physics, and we have found intriguing new phases of matter exhibiting e.g. spontaneous pattern formation. Moreover, it sparks more general theoretical questions on the role of the role of topology in non-equilibrium quantum states described by a density matrix instead of a pure state wave function [5]. The general non-equilibrium perspective may be helpful to better understand finite temperature states as well.
Figure: Upper panel: A dark state is a pure sink state in Hilbert space, into which the system's density matrix is driven under suitable conditions. This concept underlies the possiblity of creating quantum order by dissipation. Lower panel: Implementation idea with driven-dissipative ultracold atoms in an optical lattice by immersion of a coherently driven system in a bigger reservoir.
[1] S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. Büchler, P. Zoller, Quantum States and Phases in Driven Open Quantum Systems with Cold Atoms, Nature Physics 4, 878 (2008).
[2] P. Schindler, M. Müller, D. Nigg, J. T. Barreiro, E. A. Martinez, M. Hennrich, T. Monz, S. Diehl, P. Zoller, R. Blatt, Quantum simulation of open system dynamical maps with trapped ions, Nature Physics 9, 361 (2013).
[3] S. Diehl, E. Rico Ortega, M. Baranov, P. Zoller, Topology by Dissipation in Atomic Quantum Wires, Nature Physics 7, 971 (2011).
[4] S. Diehl, A. Tomadin, A. Micheli, R. Fazio, P. Zoller, Dynamical Phase Transitions and Instabilities in Open Atomic Many-Body Systems, Phys. Rev. Lett. 105, 015702 (2010).
[5] J. C. Budich, S. Diehl, Topology of Density Matrices, Phys. Rev. B 91, 165140 (2015).
Review: M. Müller, S. Diehl, G. Pupillo, P. Zoller, Engineered Open Systems and Quantum Simulations with Atoms and Ions, Advances in Atomic, Molecular and Optical Physics 61, 1-80 (2012).
Dynamics of Interacting Many-Body Systems
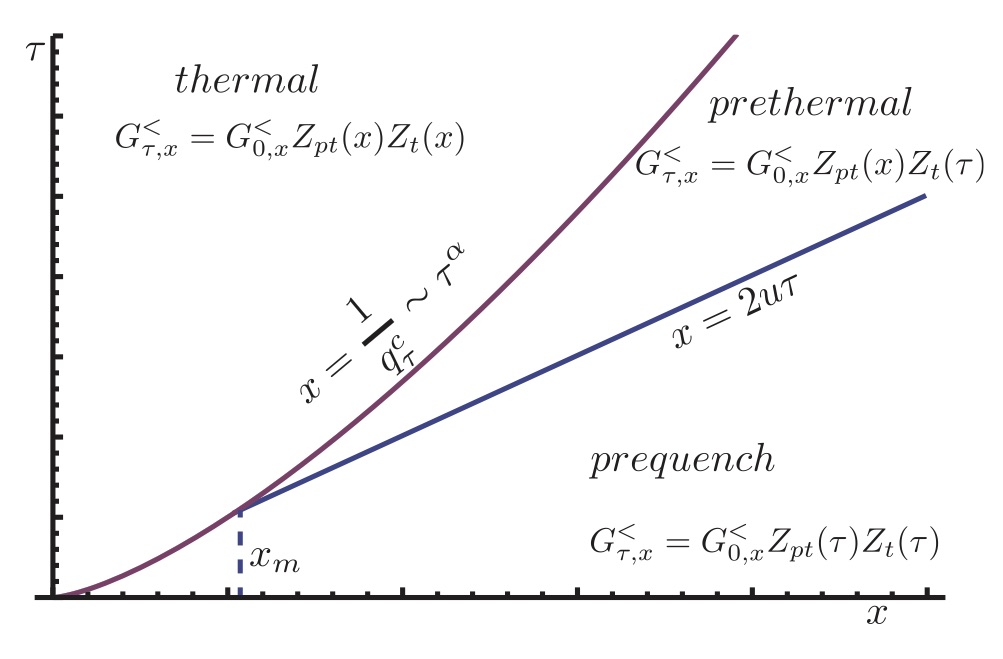
The above research topics focuses on non-equilibrium stationary states. Identifying universal properties and dynamical regimes in the time evolution of many-body systems, driven or not, represents another fascinating challenge of modern many-body physics. Ultracold atomic quantum systems are prime platforms in this respect, due to relatively long timescales, which makes it possible to track the dynamics towards the stationary state and resolve various regimes. We have studied one-dimensional systems of ultracold atoms in optical lattices based on Dyson-Schwinger equations [1], making it possible to resolve and quantitatively characterize the full sequence of dephasing, prethermalization, and thermalization stages, including the effects of slow hydrodynamic modes [2,3].
Figure: Dynamical phase diagram: temporal and spatial regimes of the time-evolving equal-time Green's function, exhibiting various dynamical regimes.
[1] M. Buchhold, S. Diehl, Kinetic Theory for Interacting Luttinger Liquids, Eur. Phys. J. D 69: 224, (2015).
[2] M. Buchhold and S. Diehl, Phys. Rev. A 92, 013603 (2015).
[3] M. Buchhold, M. Heyl, S. Diehl, Prethermalization and thermalization of a quenched interacting Luttinger liquid, Phys. Rev. A 94, 013601 (2016).
Strongly Correlated Ultracold Atoms
Ultracold atomic systems are versatile platforms to realize interesting quantum many-body systems in a highly tuneable way. A prominent example is the BCS-BEC crossover which smoothly interpolates between the two cornerstones of quantum condensation phenomena, Bose-Einstein Condensation (BEC) and BCS superfluidity of Cooper-paired fermions. It is realized in ultracold two-component fermions near a Feshbach resonance. Here we have developed a functional integral approach encompassing the complete finite temperature crossover phase diagram in the framework of various beyond mean field methods, in particular, the functional renormalization group technique [1].
Sometimes, effective equilibrium situations can be emergent from an underlying driven-open system dynamics. For example, we have shown that stable strongly correlated optical lattice models with a three-body constraint can emerge in the short time domain of systems with very strong three-body loss via the quantum Zeno effect [2]. This lead us to develop a quantum field theory approach capable to deal with the constraint in an exact way, in turn revealing interesting effects such as an emergent Ising quantum phase transition between an atomic and a dimer superfluid, and a supersolid state at strong coupling [3].
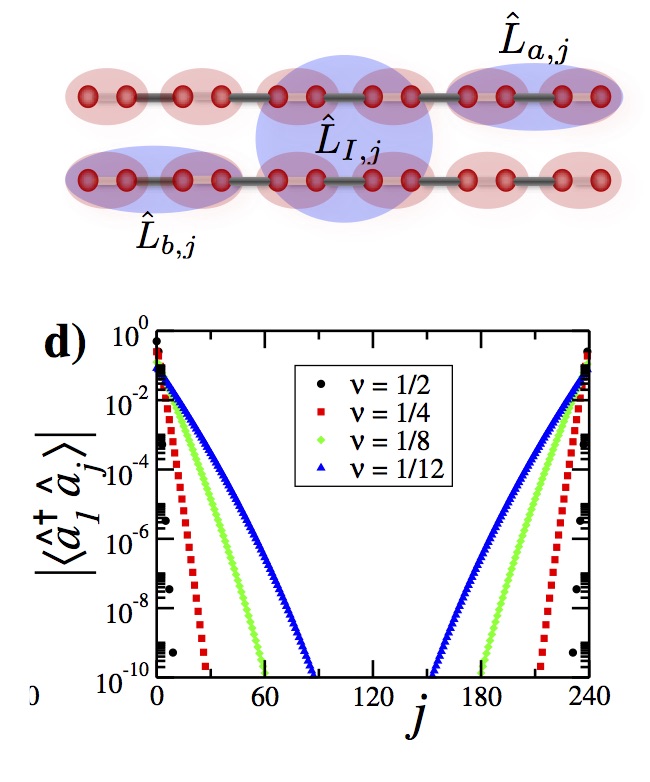
The mathematical principles governing non-equilibrium systems can also inspire progresses for equilibrium many-body physics. For example, guided by the construction of dark states in fermion systems (see "order by dissipation"), we recently established an exactly solvable number conserving model of interacting fermions in a two-wire geometry supporting nonlocal zero energy edge excitations [4]. We established their Majorana nature by devising a suitable braiding protocol. This work complements previous numerical or approximate analytical studies.
Figure: Upper panel: Support of operators each annihilating the ground state. Lower panel: analytically computed non-local correlations. They decay exponentially in the bulk, but revive at the opposite edge of the system.
[1] S. Diehl, H. Gies, J. M. Pawlowski, C. Wetterich, Flow Equations for the BCS-BEC Crossover, Phys. Rev. A 76, 021602(R) (2007).
[2] A. J. Daley, J. Taylor, S. Diehl, M. Baranov, P. Zoller, Atomic three-body loss as a dynamical three?body interaction, Phys. Rev. Lett. 102, 040402 (2009).
[3] S. Diehl, M. Baranov, A. J. Daley, P. Zoller, Observability of Quantum Criticality and a Continuous Supersolid in Atomic Gases, Phys. Rev. Lett. 104, 165301 (2010).
[4] F. Iemini, L. Mazza, D. Rossini, R. Fazio S. Diehl, Localized Majorana like modes in a number conserving setting: An exactly solvable model, Phys. Rev. Lett. 115,156402 (2015).
Review: I. Boettcher, J. M. Pawlowski, S. Diehl, Ultracold atoms and the Functional Renormalization Group, Nucl. Phys. B 228 63, (2012).