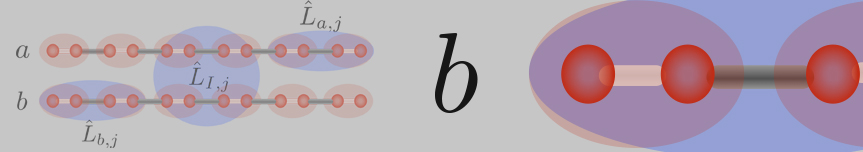research S. Diehl

THP

Research Interests

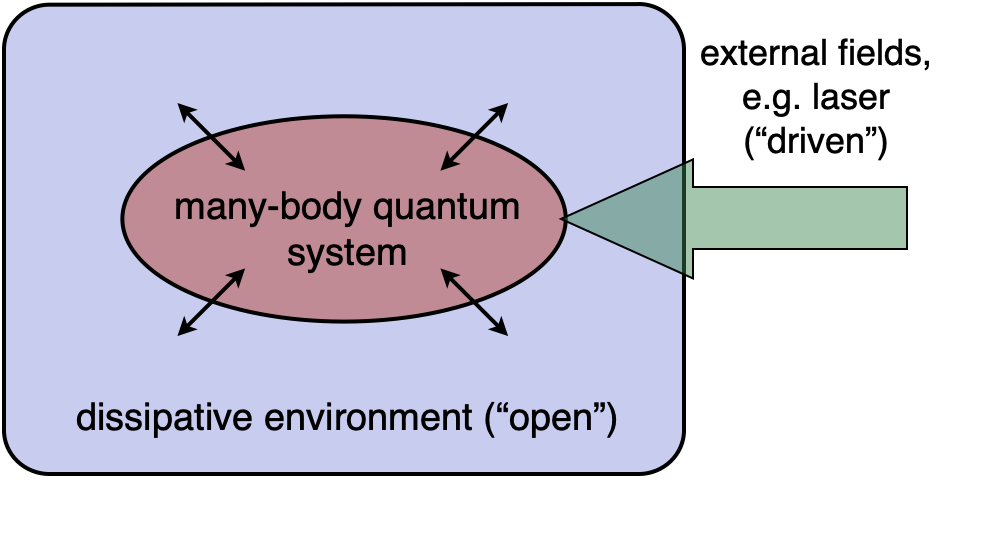
Our research focuses on driven open quantum matter, where coherent quantum dynamics coexist with external driving, dissipation, and quantum measurement. Such systems arise across platforms ranging from ultracold atomic gases and light-driven quantum materials to emerging quantum computing architectures. Their defining feature is the violation of thermodynamic equilibrium conditions at the microscopic level. Our overarching goal is to identify and understand the universal principles governing the macroscopic physics emerging from these non-equilibrium quantum dynamics.

Quantum field theory out of equilibrium

In driven open quantum systems, many standard tools of equilibrium many-body physics fail due to the absence of microscopic detailed balance. We therefore develop theoretical frameworks that combine concepts from quantum optics, solid-state physics, and quantum field theory. A central approach is the formulation of these systems using the Keldysh functional integral (see [1]). This framework opens the toolbox of quantum field theory to non-equilibrium settings, including diagrammatic methods and renormalization-group techniques for quantitative analysis [2-4]. Beyond its practical utility, it provides a unifying conceptual language based on symmetries and conservation laws [1]. Within this perspective, the distinction between equilibrium and non-equilibrium physics itself can be expressed in terms of symmetry [5,6].

[1] L. M. Sieberer, M. Buchhold, S. Diehl, Keldysh Field Theory for Driven Open Quantum Systems, Rep. Prog. Phys. 79, 096001 (2016), arxiv:1512.00637.
[2] L. M. Sieberer, S. D. Huber, E. Altman, S. Diehl, Non-equilibrium Functional Renormalization for Driven-Dissipative Bose-Einstein Condensation, Phys. Rev. B 89, 134310 (2014), arxiv:1309.7027.
[3] M. Buchhold, B. Everest, M. Marcuzzi, I. Lesanovsky, S. Diehl, Non-equilibrium effective field theory for absorbing state phase transitions in driven open quantum spin systems, Phys. Rev. B 95, 014308 (2017) (Editor's Suggestion), arxiv:1611.02283.
[4] C. P. Zelle, R. Daviet, A. Rosch, S. Diehl, Universal phenomenology at critical exceptional points of nonequilibrium O(N) models, Phys. Rev. X 14, 021052 (2024), arxiv:2304.09207.
[5] L. M. Sieberer, A. Chiocchetta, A. Gambassi, U. C. Täuber, S. Diehl, Thermodynamic Equilibrium as a Symmetry of the Schwinger-Keldysh Action, Phys. Rev. B 92,134307 (2015), arxiv:1505.00912.
[6] A. Altland, M. Fleischhauer, S. Diehl, Symmetry classes of open fermionic quantum matter, Phys. Rev. X 11, 021037 (2021), arxiv:2007.10448.

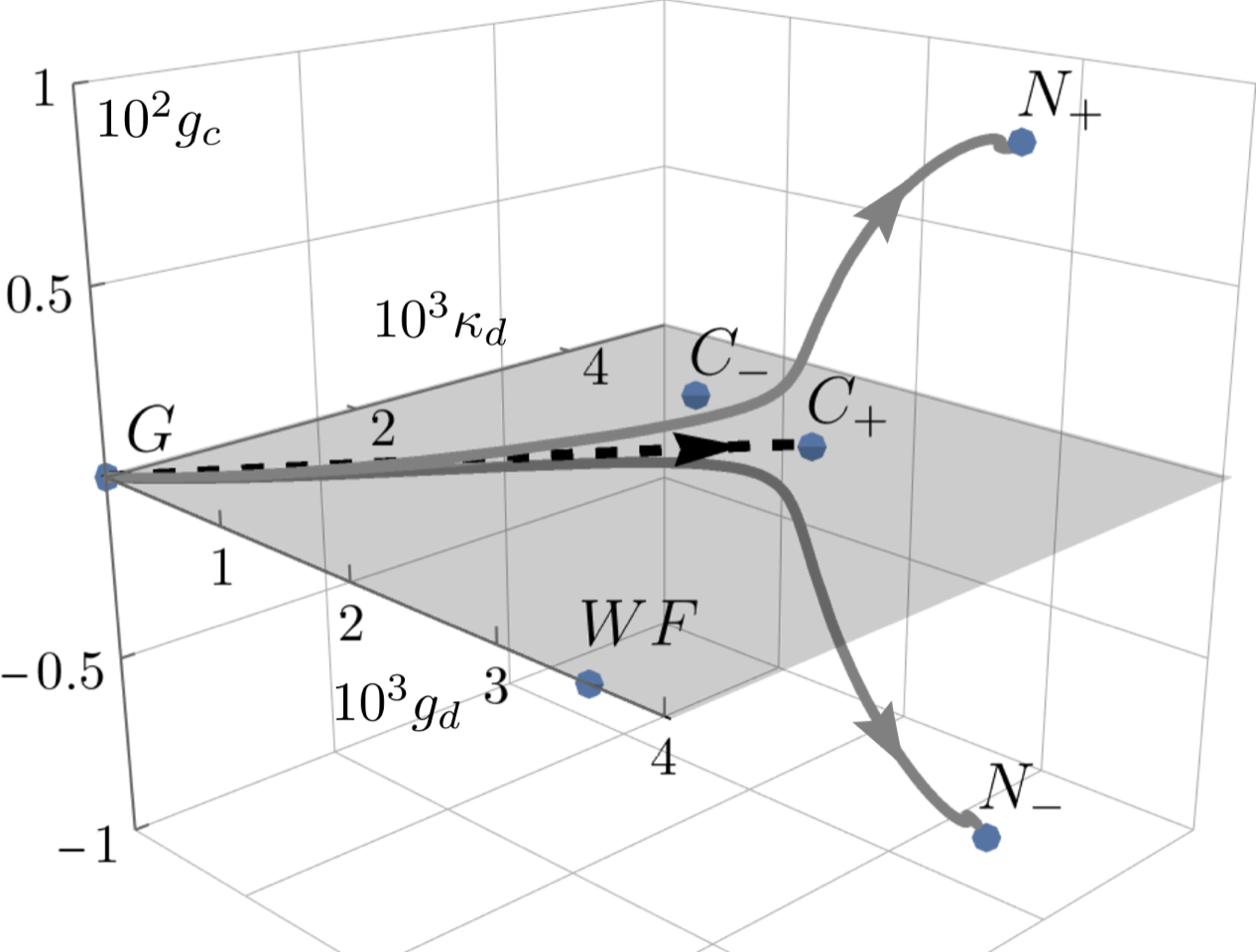
Universal phenomena in driven open quantum matter

Universality refers to the insensitivity of macroscopic observables to microscopic details. Near second-order phase transitions, for example, vastly different systems fall into a small number of universality classes. Similar behavior appears in ordered phases and in dynamical phenomena governed by conservation laws. One might therefore expect microscopic violations of equilibrium to be irrelevant at large scales. We show that this expectation is not generally valid; see [1] for a review. Instead, broken equilibrium conditions can give rise to new forms of universality without equilibrium counterparts [2,3]. We place particular emphasis on intrinsically quantum effects, for example in driven open [4, 5] and monitored quantum matter [6], and connect these insights to experiments in cold-atom [7] and solid-state platforms [8].

[1] L. M. Sieberer, M. Buchhold, J. Marino, S. Diehl, Universality in driven open quantum matter, Rev. Mod. Phys. 97, 025004 (2025), arxiv:2312.03073.
[2] L. Sieberer, S. Huber, E. Altman, S. Diehl, Dynamical critical phenomena in driven-dissipative systems, Phys. Rev. Lett. 110 195301 (2013), arxiv:1301.5854.
[3] R. Daviet, C. P. Zelle, A. Rosch, S. Diehl, Non-equilibrium criticality at the onset of time-crystalline order in O(N) models, Phys. Rev. Lett. 132, 167102 (2024), arxiv:2312.13372.
[4] J. Marino, S. Diehl, Driven Markovian Quantum Criticality, Phys. Rev. Lett. 116, 070407 (2016), arxiv:1508.02723.
[5] R. Mittal, T. Zander, J. Lang, Sebastian Diehl, Fermion quantum criticality far from equilibrium, arxiv:2507.14318.
[6] M. Buchhold, Y. Minoguchi, A. Altland, S. Diehl, Effective Theory for the Measurement-Induced Phase Transition of Dirac Fermions, Phys. Rev. X 11, 041004 (2021), arxiv:2102.08381.
[7] S. Helmrich, A. Arias, G. Lochead, T.M. Wintermantel, M. Buchold, S. Diehl and S. Whitlock, Signatures of self-organized criticality in an ultracold atomic gas. Nature (2020), arxiv:1806.09931.
[8] S. Widmann, S. Dam, J. Düreth, C. Mayer, R. Daviet, C. Zelle, D. Laibacher, M. Emmerling, M. Kamp, S. Diehl, S. Betzold, S. Klembt, S. Höfling, Observation of Kardar-Parisi-Zhang universal scaling in two dimensions, arxiv:2506.15521.

Topology beyond ground states

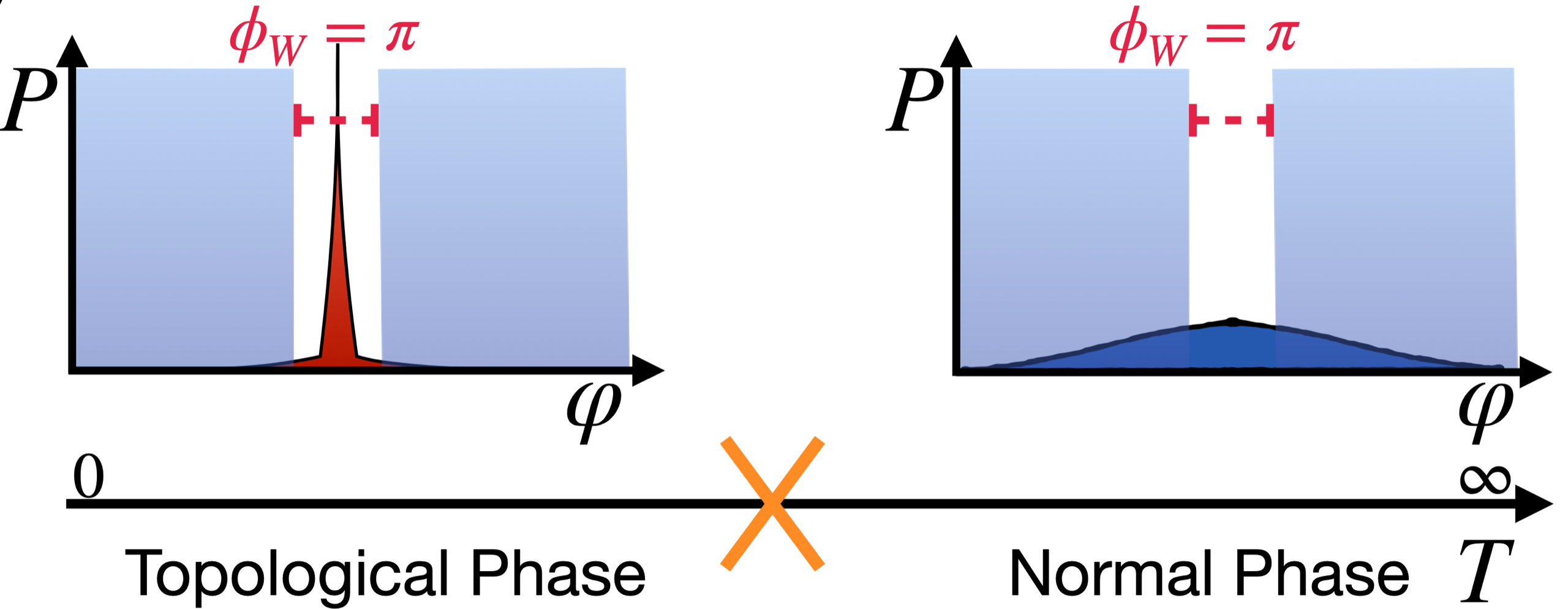
Topological concepts have transformed our understanding of quantum matter, explaining quantized observables such as the Hall conductance and characterizing broad classes of insulating and superconducting phases. Most work has focused on ground states of Hamiltonian equilibrium systems. In realistic settings, however, quantum systems operate at finite temperature and often under dissipation and decoherence. We investigate topological phenomena in mixed quantum states [1] and in out-of-equilibrium regimes [2]. Our research examines to what extent topology remains a source of universality [3], which observables can probe this physics [4], and how robust quantum information is under such conditions [5]. We also study novel topological phase transitions without equilibrium or ground-state counterparts [6,7].

[1] J. C. Budich, S. Diehl, Topology of Density Matrices, Phys. Rev. B 91, 165140 (2015), arXiv:1501.04135.
[2] F. Tonielli, J. C. Budich, A. Altland, S. Diehl, Topological Field Theory far from Equilibrium, Phys. Rev. Lett. 124, 240404 (2020), arxiv:1911.07834.
[3] Z. Huang, X. Sun, Sebastian Diehl, Topological gauge theory for mixed Dirac stationary states in all dimensions, Phys. Rev. B 106, 245204 (2022), arxiv:2109.06891.
[4] C. E. Bardyn, L. Wawer, A. Altland, M. Fleischhauer, S. Diehl, Probing the topology of density matrices, Physical Review X 8 (2018), arxiv:1706.02741.
[5] Z. Huang, L. Colmenarez, M. Müller, S. Diehl, Coherent information as a mixed-state topological order parameter of fermions, Phys. Rev. Research 7, 043009 (2025), arxiv:2412.12279.
[6] Z. Huang, S. Diehl, Interaction-Induced Topological Phase Transition at Finite Temperature, Phys. Rev. Lett. 134, 053002 (2025) (Editors' Suggestion), arxiv:2407.04779.
[7] L. He, L. M. Sieberer, S. Diehl, Space-time vortex driven crossover and vortex turbulence in one-dimensional driven open condensates, Phys. Rev. Lett. 118, 085301 (2017), arxiv:1607.06451.

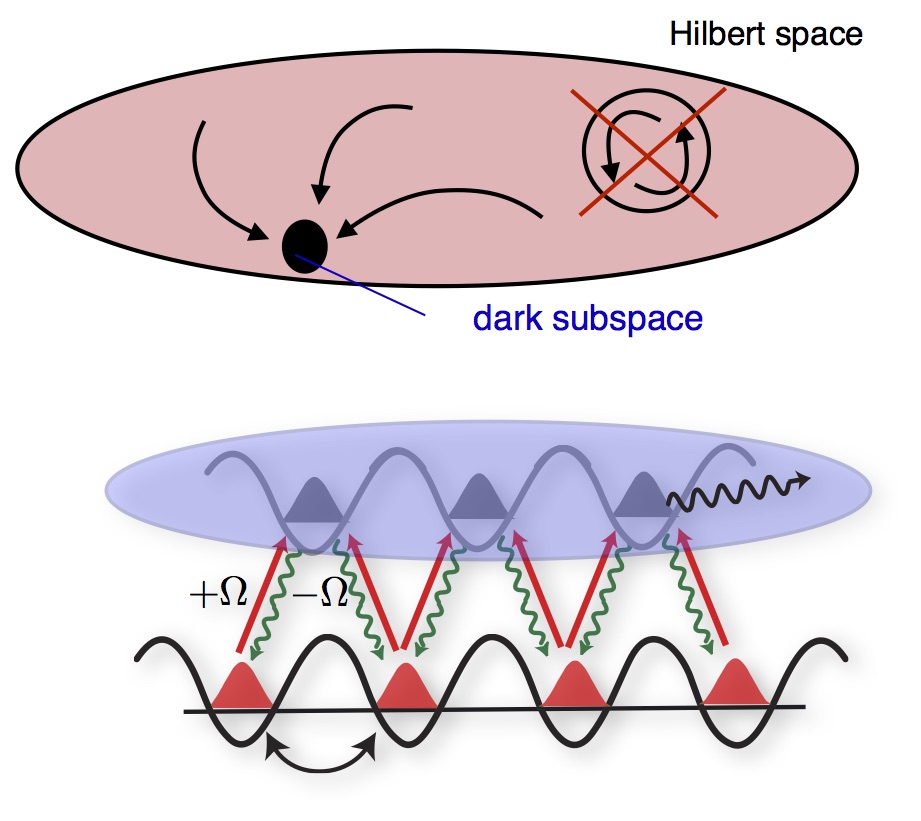
Quantum engineering for cold atoms, solid-state systems, and related platforms

Modern platforms in cold-atom physics, quantum materials, and qubit-based architectures provide unprecedented control over microscopic dynamics, often beyond equilibrium Hamiltonian descriptions. We explore how such control can be used to engineer novel states and phases of matter far from equilibrium. Examples include noise-resilient mechanisms for stabilizing time-crystalline order, where an order parameter exhibits persistent temporal oscillations even in a stationary state [1], the realization of Kardar-Parisi-Zhang universality in Josephson junction arrays [2], or the stabilization of quantum spin liquids by rapid Floquet drive [3]. More broadly, our work demonstrates that noise and dissipation need not be detrimental to quantum correlations [4]. When properly combined with external driving, they can instead serve as resources for generating quantum order, including phase coherence [5], entanglement [6], and topological order [7].

[1] C. Zelle, R. Daviet, A. Millis, S. Diehl, Nonequilibrium orders in parametrically driven field theories, arxiv:2506.18622.
[2] M. Tsitsishvili, R. Egger, K. Flensberg, S. Diehl, From Kardar-Parisi-Zhang scaling to soliton proliferation in Josephson junction arrays, Phys. Rev. Lett. 135, 246001 (2025), arxiv:2509.08479 .
[3] A. Chiocchetta, D. Kiese, F. Piazza, S. Diehl, Cavity-induced quantum spin liquids, Nature Communications 12, 5901 (2021), arxiv:2009.11856.
[4] M. Müller, S. Diehl, G. Pupillo, P. Zoller, Engineered Open Systems and Quantum Simulations with Atoms and Ions, Advances in Atomic, Molecular and Optical Physics 61, 1-80 (2012), arxiv:1203.6595.
[5] S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. Büchler, P. Zoller, Quantum States and Phases in Driven Open Quantum Systems with Cold Atoms, Nature Physics volume 4, pages 878–883 (2008), arxiv:0803.1482.
[6] P. Schindler, M. Müller, D. Nigg, J. T. Barreiro, E. A. Martínez, M. Hennrich, T. Monz, S. Diehl, P. Zoller, R. Blatt, Quantum simulation of dynamical maps with trapped ions, Nature Physics volume 9, pages 361–367 (2013), arxiv:1212.2418.
[7] S. Diehl, E. Rico Ortega, M. Baranov, P. Zoller, Topology by Dissipation in Atomic Quantum Wires, Nature Physics volume 7, pages 971–977 (2011), arxiv:1105.5947.