Equilibrium Statistical Mechanics and Field Theory
Sequence alignment is the most widely used data analysis tool in molecular biology. Detecting and quantifying sequence similarities is an intricate statistical problem, which has profound connections to the statistical physics of systems with quenched disorder. Other projects in this area are concerned with long-range correlations in genomes and with the statistics of RNA secondary structures.
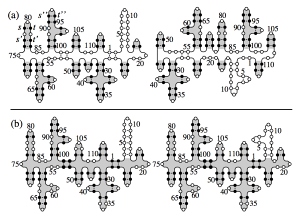
The secondary structure of a random RNA molecule is frozen at low temperatures (a) and molten at higher temperatures (b).
Selected physics publications
Delocalization transitions of semiflexible manifolds
R. Bundschuh and M. Lässig, Phys. Rev. E65, 61502, (2002)
Semiflexible manifolds such as fluid membranes or semiflexible polymers undergo delocalization transitions if they are subject to attractive interactions. We study manifolds with short-ranged interactions by field-theoretic methods based on the operator product expansion of local interaction fields. We apply this approach to manifolds in a random potential. Randomness is always relevant for fluid membranes, while for semiflexible polymers there is a first-order transition to the strong coupling regime at a finite temperature.
Vicinal surfaces and the Calogero-Sutherland model
M. Lässig, Phys. Rev. Lett. 77, 526, (1996)
A miscut (vicinal) crystal surface can be regarded as an array of meandering but noncrossing steps. Interactions between the steps are shown to induce a faceting transition of the rough surface between a homogeneous Tomonaga-Luttinger liquid state and a low-temperature regime of local step clusters in coexistence with ideal facets. This morphological transition is governed by a hitherto neglected critical line of the well-known Calogero-Sutherland model. Its exact solution yields expressions for measurable quantities that compare favorably with recent experiments on Si surfaces.
Geometry of the renormalization group, with an application in two dimensions
M. Lässig, Nucl. Phys. B334, 652, (1990)
The renormalization group is viewed as a theory of the geometry of action space. A general covariant relation between coupling constant and field renormalization is derived. As an application, the crossover between the two-dimensional minimal modes M
m and M
m−1 is calculated to two-loop order in a minimal subtraction scheme.
Selected applications to biology and bioinformatics
Freezing of random RNA
M. Lässig and K. Wiese, Phys. Rev. Lett. 96, 228101, (2006)
We study secondary structures of random RNA molecules by means of a renormalized field theory based on an expansion in the sequence disorder. We show that there is a continuous phase transition from a molten phase at higher temperatures to a low-temperature glass phase. The primary freezing occurs above the critical temperature, with local islands of stable folds forming within the molten phase. The size of these islands defines the correlation length of the transition. Our results include critical exponents at the transition and in the glass phase.
Correlated Random Networks
J. Berg and M. Lässig, Phys. Rev. Lett. 89, 228701, (2002)
We develop a statistical theory of networks. A network is a set of vertices and links given by its adjacency matrix c, and the relevant statistical ensembles are defined in terms of a partition function Z=Σexp([-βH(c)]. The simplest cases are uncorrelated random networks such as the well-known Erdös-Rényi graphs. Here we study more general interactions H(c) which lead to correlations, for example, between the connectivities of adjacent vertices. In particular, such correlations occur in optimized networks described by partition functions in the limit β --> infinity. They are argued to be a crucial signature of evolutionary design in biological networks.
go back 


