Research

Our overarching goal is to explore and understand the microscopic mechanisms behind emergent, collective phenomena in Quantum Materials—ranging from magnetism, bad and strange metallicity, to high-temperature superconductivity. In this endeavor, we often deal with strongly correlated electron systems and face the so-called quantum many-body problem: an incredibly large number of quantum particles—electrons—behave in a highly interdependent manner. Such problems cannot be solved exactly (we couldn’t even store the full solution in classical bits using all atoms of the universe); instead, one needs approximate and often numerical approaches. What’s more, we aim to describe and predict spectroscopic and transport properties of correlated electrons, which are fundamental probes for experimentalists but among the most challenging problems for theorists. So, how do we deal with this?

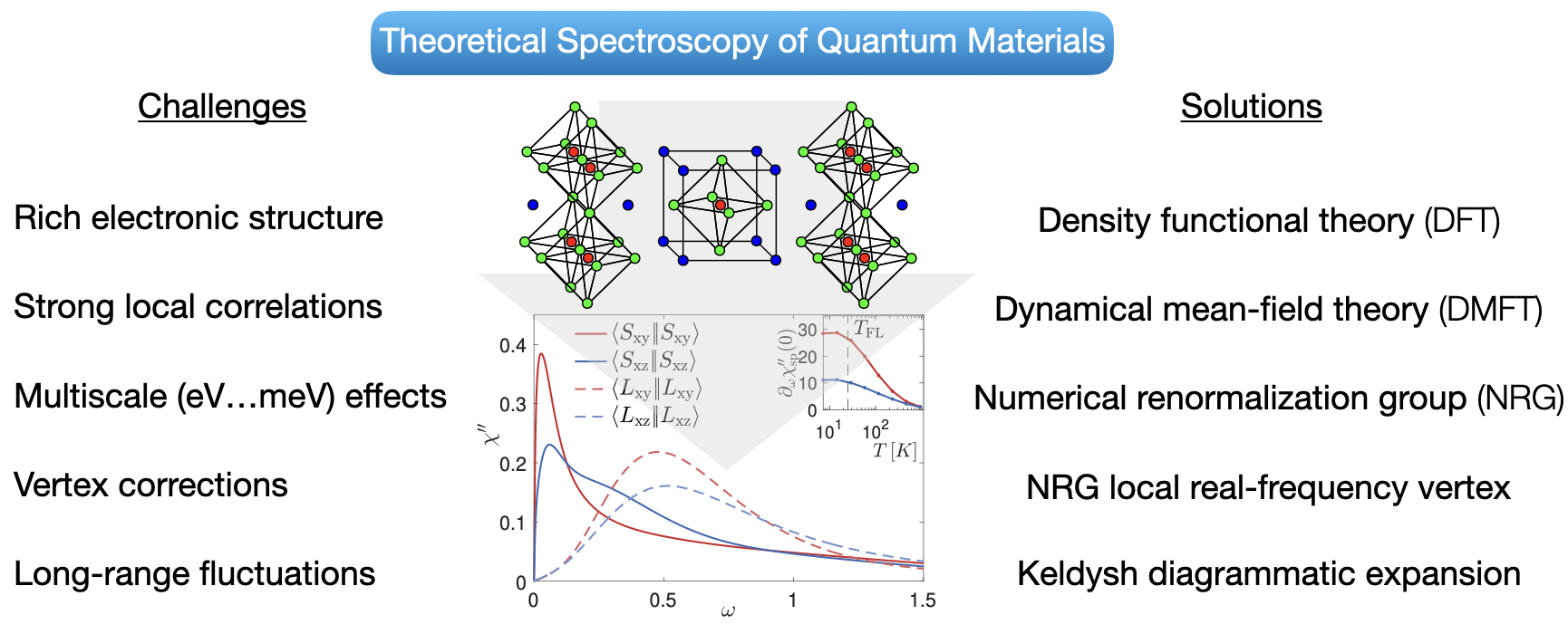We use a multi-method approach. As is common in the field, electronic structure methods allow us to reduce the complexities of a given material to a generalized, multiorbital Hubbard model. Then, the dynamical mean-field theory maps this model onto a so-called quantum impurity model. Now, this is a system we can solve exactly. In fact, using the numerical renormalization group, we even obtain such a solution in real frequencies—opposed to the widely used imaginary-time simplification. This real-frequency information is our starting point to study spectroscopy and transport. If needed, we further employ Keldysh quantum field theory methods to additionally incorporate long-range fluctuations.

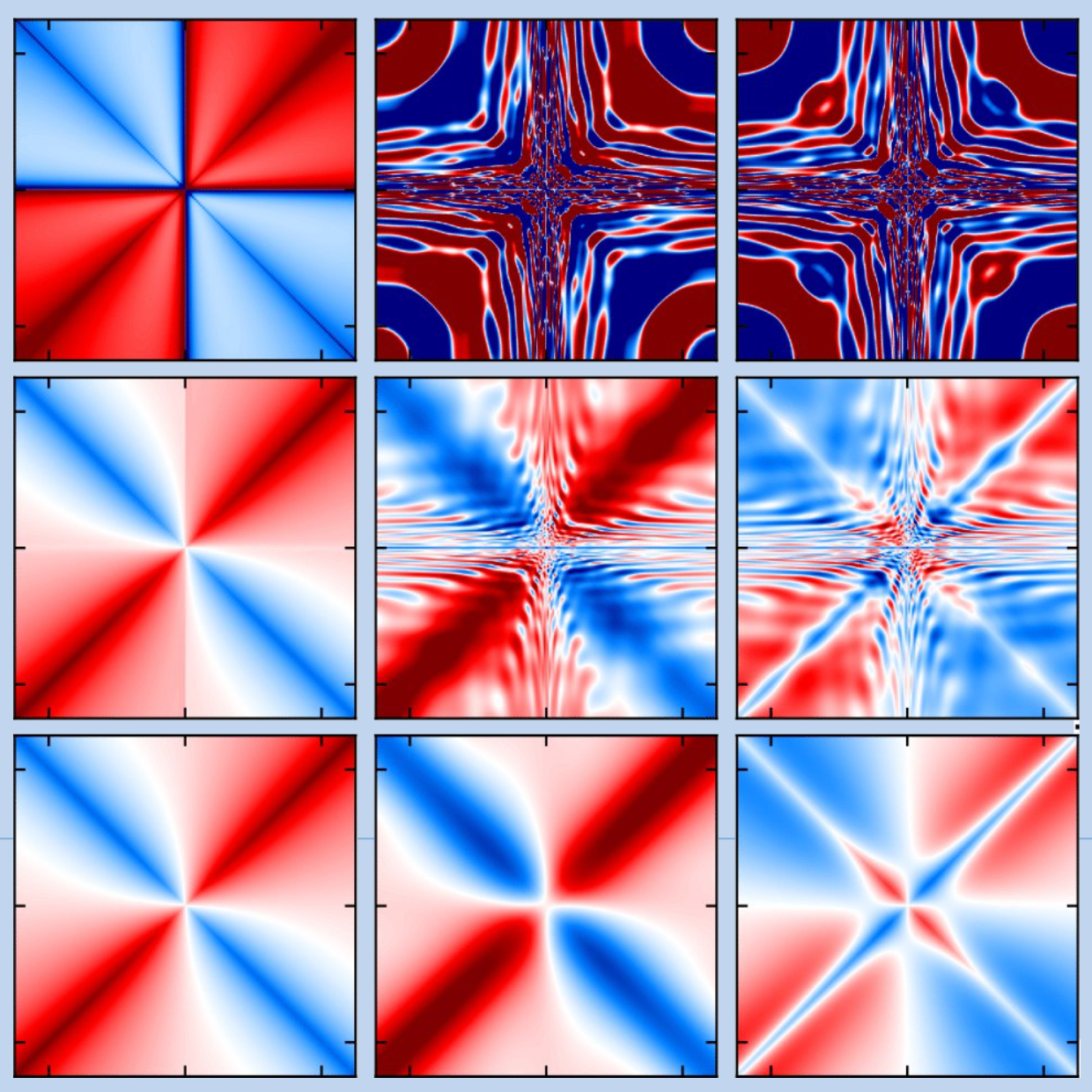We want to build the best methods to answer the most pressing questions! This often involves analytic (pen and paper) algorithmic development. We try to leverage the many-body toolbox as much as possible. Concepts like the renormalization group, diagrammatic resummations, spectral representations, or tensor networks are part of our every-day language. By implementing these algorithms numerically, we can simulate quantum systems and predict material properties. Turning different knobs in the simulation, we can distill the microscopic mechanisms behind individual phenomena. An example for the fruitful interplay of analytical and numerical development is our work on four-point vertices, which was featured on the cover of the 2024 LRZ high-performance computing booklet: We first used equations of motion to derive analytically equivalent but numerically more robust expressions for multipoint vertices. After carefully implementing the new expressions, we ran them on a supercomputer and obtained results of unprecedented quality.

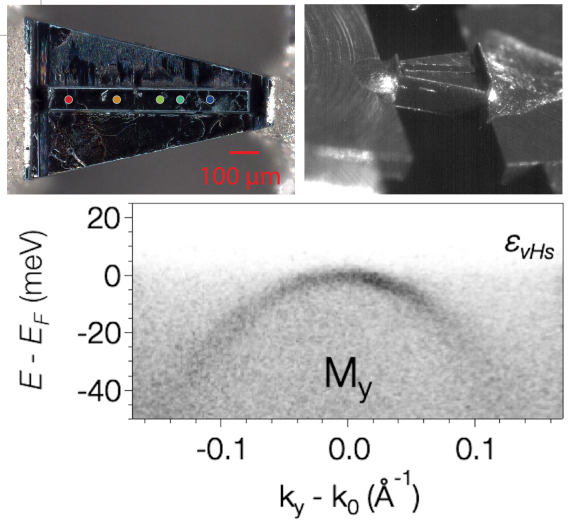In some cases, we try to understand the salient features of strongly correlated electrons from paradigmatic models. In other cases, we aim for accurate predictions of material properties and want to put our theory to the most stringent test. To this end, we seek the comparison to experiment as much as possible. For instance, we collaborate with the group of Felix Baumberger in Geneva, Switzerland, on angle-resolved photoemission spectroscopy of Sr₂RuO₄ (see arXiv:2503.11311).