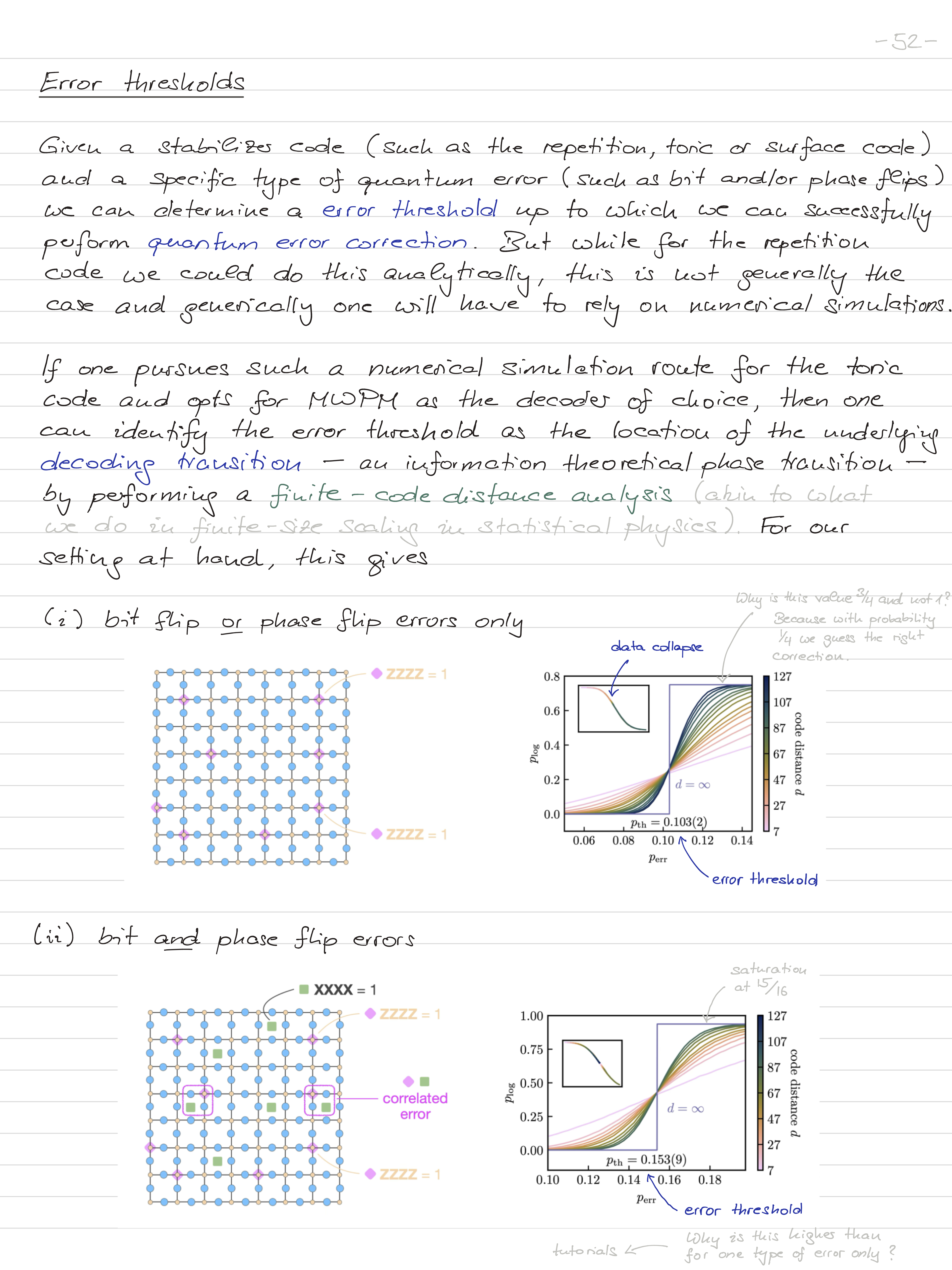
Quantum Computational Physics
fall 2024
Tue, 10.00 | weekly lecture
S. Trebst, E0.03 (ETP)
Fri, 10.00 | biweekly lecture
S. Trebst, E0.03 (ETP)
Fri, 10.00 | biweekly tutorial
F. Eckstein, M. Pütz, Q. Preiss, E0.03 (ETP)
lecture dates: Oct 8, 11, 22, 29; Nov 5, 12, 15, 22, 26; Dec 10, 17; Jan 7, 14, 24, 28
tutorial dates: Oct 15, 25; Nov 8, 19; Dec 3, 20; Jan 17, 31
Overview
The lecture will introduce concepts, algorithms, and practical computational skills to simulate quantum many-body systems on digital quantum computing platforms that have become broadly accesible in recent years (such as the cloud-accessible processors from IBM Quantum, AWS Braket, or Microsoft Azure Quantum).As such this lecture aims to complete a "trifecta" of our computational physics curriculum of a bachelor-level computational physics course (mostly addressing single- and few-particle physics), a master-level computational many-body physics course (addressing how to simulate classical and quantum many-body systems on classical compute hardware) with a course doing "quantum on quantum".
This course will not teach high-level quantum algorithms (aimed at revolutionizing, e.g., quantum chemistry calculations) nor intermediate-level quantum simulations (aiming to bring, say, the Hubbard model onto a quantum computer), but will aim at the "assembler-level" of quantum computing, asking what kind of quantum many-body phenomena one can induce in digital quantum circuits that employ not only the conventional set of unitary gates, but also mid-circuit measurements and active feedback.
Please sign up for this course via its ILIAS entry,
which will help us in coordinating this course and its tutorials.
Lectures
Lecture weeks (toggle):
week 1+2 |
week 3+4 |
week 5+6 |
week 7+8 |
week 9+10 |
week 11+12 |
week 13+14
Week 11 (January 6, 2025)

- lecture notes: Random unitary circuits: unitary circuits, thermalization & entanglement dynamics, random circuits, entanglement growth
Week 12 (January 13, 2025)
- lecture notes: Geometry of entanglement: minimal cut, KPZ physics
- tutorial: QuantumClifford.jl, Entanglement pyramid, Measurement-induced phase transition
Week 13 (January 20, 2025)

- lecture notes: Measurement-induced phase transition: entangling vs. disentangling forces, scrambling & volume-law stability, critical dynamics, minimal cut, percolation
Week 14 (January 27, 2025)

- lecture notes: Measurement-only dynamics: monitored transverse-field Ising model, entanglement phase transition & percolation, scrambling and unscrambling by measurement, monitored Kitaev model
- tutorial: The monitored trasverse-field Ising model, the monitored Kitaev model
Syllabus
- part A:
fundamentals
quantum circuits
quantum measurements
entanglement structures
pure and mixed states
mixed state topology
geometry of entanglement
- part B:
quantum state preparation (shallow circuits)
toric code / quantum memory / long-range entanglement
surface code and many-body teleportation
Nishimori's cat (weak measurement)
non-Abelian topological order
time crystals
- part C:
entanglement dynamics (deep circuits)
random unitery circuits
measurement-induced phase transitions
Kitaev circuits / Hastings-Haah code
qubit fractionalization
Literature
General textbooks- Thomas Wong, Introduction to Classical and Quantum Computing (self-published)
- Nielsen and Chuang, Quantum Computation and Quantum Information, Cambridge University Press
available in physics student library, university library - N. David Mermin, Quantum Computer Science, Cambridge University Press
available in physics student library, university library
General references
- Quantum algorithms: A survey of applications and end-to-end complexities, arXiv:2310.03011 This is a survey of the high-level quantum algorithms (requiring millions of qubits) that will not be covered in this lecture.
- Quantum Error Correction For Dummies, arXiv:2304.08678
- Error Correction Zoo, errorcorrectionzoo.org If you want to look beyond the repetition/surface/toric code and the Steane code discussed in the lecture, here are 566 classical and quantum codes. And it is still expanding...
Programming resources on the web
- IBM Quantum, Qiskit
- Clifford simulations: STIM,
QuantumClifford.jl
quantum computing in 2024 - selected publications
- Nishimori transition: arXiv:2309.02863, and Nature Physics (2024)
- Repetition code: arXiv:2409.13025
- Surface code: arXiv:2408.13687, and Nature (2024)
- Steane code: arXiv:2312.03982, and Nature 626, 58 (2024)
Prerequisites
This specialized course is intended for master students; it builds on a bachelor level introduction to quantum mechanics and computational physics as it is taught in many places around the world. Prior attendance of the master-level courses on computational many-body physics and quantum information theory will be a plus.We also expect you to have light programming experience, though not in any specific programming language.