Research

Disclaimer: The content of this page is currently under revision and will be updated shortly.

Our group studies collective phenomena in quantum many-body systems that arise in the presence of strong correlations. In our work we typically complement analytical approaches by a variety of sophisticated numerical techniques that exploit concepts from statistical physics, quantum information theory, and computer science.

The following sections give an overview of the major lines of our research in the past 3 to 5 years:


Some of our long-term favorites:


Quantum spin liquids and Majorana metals

One of the most intriguing phenomena in strongly correlated systems is the fractionalization of quantum numbers – familiar examples include the spin-charge separation in one-dimensional metallic systems, the fractionalization of the electron in certain quantum Hall states or the emergence of monopoles in spin ice.

The hyperoctagon lattice is a three-dimensional tricoordinated lattice with space group symmetries I4132 (no. 241). In this line of research, which is largely a collaboration with Maria Hermanns, we investigate the fractionalization of magnetic moments in three-dimensional Kitaev models. Our interest currently focuses on the collective behavior of the emergent Majorana fermionic degrees of freedom, which form (semi)metallic states whose precise character turns out to intimately depend on the underlying lattice structure. For the two-dimensional honeycomb Kitaev model it is well known that the Majorana fermions form a semimetal with two gapless Dirac points. For three-dimensional lattices (that preserve the tricoordination of the vertices) one finds Majorana metals with a two-dimensional Fermi surface akin to a conventional metal [1], states with nodal lines or even topological semimetals with Weyl nodes [2]. Going beyond the Kitaev model and considering the effects of interactions between the Majoranas, we could show that some of these systems generically undergo a spin-Peierls transition [3].

These 3D Kitaev models thus host an unusually rich variety of Z2 spin liquids that are all analytically tractable. Discovering such spin liquid physics in an actual material should be a strong motivation to study spin-orbit entangled Mott insulators such as the recently synthesized Iridate compounds β-Li2IrO3 and γ-Li2IrO3, which potentially realize such 3D Kitaev models (see also the next section).

References
[1] Maria Hermanns and Simon Trebst, Phys. Rev. B 89, 235102 (2014).
[2] Maria Hermanns, Kevin O' Brien, and Simon Trebst, Phys. Rev. Lett. 114, 157202 (2015).
[3] Maria Hermanns, Simon Trebst, and Achim Rosch, Phys. Rev. Lett. 115, 177205 (2015).
[4] Kevin O' Brien, Maria Hermanns, and Simon Trebst, Phys. Rev. B 93, 085101 (2016).

 Other resources
[5] Video and slides from a talk on Spin-Peierls Instabilities of 3D Kitaev Spin Liquids at KITP in fall 2015
[6] Slides from a talk on Majorana metals in spin-orbit entangled quantum matter given at the 2015 APS March Meeting
[7] Three-dimensional prints of these three-dimensional, tricoordinated lattices are available via shapeways.
[8] VESTA files for these three-dimensional, tricoordinated lattices: (10,3)a, (10,3)b, (10,3)c, (9,3)a, (8,3)a, (8,3)b, (8,3)c, (8,3)n


Spin-orbit entanglement in Iridates

The physics of transition metal oxides with partially filled 5d shells is governed by a largely accidental balance of electronic correlations, spin-orbit entanglement, and crystal field effects, with all three components coming up roughly equal in strength. With different materials exhibiting slight tilts towards one of the three effects a remarkably broad variety of quantum states has recently been suggested. A particularly intriguing scenario is the formation of Mott insulators in which the local moments are spin-orbit entangled Kramers doublets. An example are the j=1/2 Mott insulators observed for a number of Iridates including the layered materials Na2IrO3, α-Li2IrO3 (both hexagonal) and Ba3IrTi2O9 (triangular), which have been in the focus of our work.

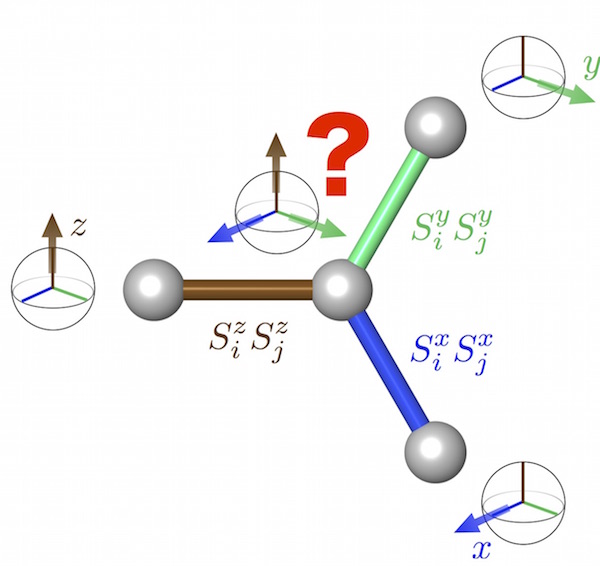
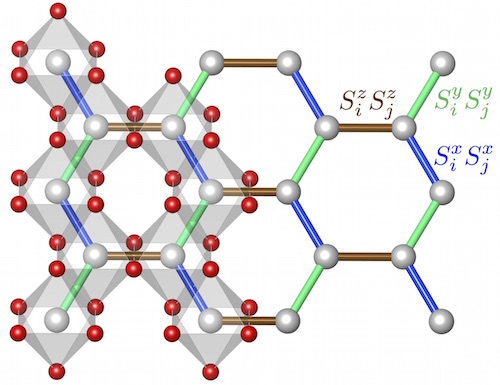The iridates Na<sub>2</sub>IrO<sub>3</sub> and α-Li<sub>2</sub>IrO<sub>3</sub> realize Kitaev-type exchange interactions The microscopic exchange in these systems has been argued to be a combination of isotropic Heisenberg and highly anisotropic Kitaev exchange, which can be tracked back to the spin and orbital components of the effective momenta. Depending on the relative strength of these two couplings, the system exhibits either various types of conventional magnetic order or a more exotic gapless spin-liquid ground state (see also the previous section). Carefully studying the stability of these phases at finite-temperatures and the role of frustration, Exchange frustration i.e. a considerable suppression of the ordering temperature from the Curie-Weiss temperature allowed us to connect back to thermodynamic experiments on the Iridates (Na,Li)2IrO3 and possibly estimate microscopic coupling parameters. Finally, we discuss the effects of a magnetic field applied in the [111] direction – perpendicular to the hexagonal lattice formed by the Iridium moments – and show that a topologically ordered ground state is found over a small range of coupling parameters [5], also indicating the existence of an exotic critical point whose location might not be far from actual material parameters.

References
[1] M. Becker, M. Hermanns, B. Bauer, M. Garst, and S. Trebst, Phys. Rev. B 91, 155135 (2015).
[2] Eran Sela, Hong-Chen Jiang, Max H. Gerlach, and Simon Trebst, Phys. Rev. B 90, 035113 (2014).
[3] Y. Singh, S. Manni, J. Reuther, T. Berlijn, R. Thomale, W. Ku, S. Trebst, and P. Gegenwart, Phys. Rev. Lett. 108, 127203 (2012).
[4] J. Reuther, R. Thomale, and S. Trebst, Phys. Rev. B 84, 100406(R) (2011).
[5] Hong-Chen Jiang, Zheng-Cheng Gu, Xiao-Liang Qi, and Simon Trebst, Phys. Rev. B 83, 245104 (2011).

 Other resources
[6] Overview article (with Kai Schmidt) on Topologische Spinflüssigkeiten in the April 2015 edition of the German Physik Journal
[7] News & Views article (with Philipp Gegenwart) on Kitaev matter in the May 2015 edition of Nature Physics


Entanglement in quantum many-body systems

References
[1] Peter Broecker and Simon Trebst, J. Stat. Mech. P08015 (2014).
[2] Peter Broecker and Simon Trebst, Phys. Rev. B 94, 075144 (2016).
[3] Maria Hermanns and Simon Trebst, Phys. Rev. B 89, 205107 (2014).
[4] Johannes Helmes, Jean-Marie Stephan, and Simon Trebst, Phys. Rev. B 92, 125144 (2015).



Topological order and quantum criticality

Even in the absence of spontaneous symmetry breaking interacting quantum many-body systems can exhibit a phase transition into an ordered phase, albeit with an unusual form of non-local order typically refered to as topological order. We have been investigating various aspects of the quantum phase transitions that occur when such a system is driven out of the topologically ordered state by competing interactions, disorder or other sufficiently strong perturbations. Specific examples for these phase transitions occur in certain quantum spin models, which we have studied by extensive numerical simulations, and range from cases exhibiting well understood quantum critical behavior – including so-call conformal quantum critical points – to cases for which our numerics suggests quantum critical behavior, but which currently lack analytical understanding.

References
[1] B. Bauer, L. Cincio, B. Keller, M. Dolfi, G. Vidal, S. Trebst, and A. Ludwig, Nature Comm. 5, 5137 (2014) and arXiv:1401.3017
[2] S.V. Isakov, P. Fendley, A.W.W. Ludwig, S. Trebst, and M. Troyer, Phys. Rev. B 83, 125114 (2011).
[3] C. Gils, S. Trebst, A. Kitaev, A. Ludwig, M. Troyer, and Z. Wang Nature Physics 5, 834 (2009) and arXiv:0906.1579
[4] Simon Trebst, Philipp Werner, Matthias Troyer, Kirill Shtengel, and Chetan Nayak, Phys. Rev. Lett. 98, 070602 (2007).

 Other resources
[5] C. Castelnovo, S. Trebst, and M. Troyer, book chapter in "Understanding Quantum Phase Transitions" (Taylor and Francis, 2010)


Open source codes for strongly correlated systems

A major part of our research is devoted to the development, implementation, and application of numerical methods for physical systems. Over the last years we have comprehensively used and further improved various computational methods including several flavors of quantum and classical Monte Carlo simulations, density matrix renormalization group calculations, exact diagonalization techniques, and high-order strong coupling expansions. We implemented all these methods exploiting modern programming techniques such as object-oriented programming in C++, generic algorithms, and parallelization schemes. We strive to facilitate the applicability of these numerical methods across disciplines such as condensed matter theory, materials research, chemical engineering, and quantum information processing.

ALPS (Algorithms and Libraries for Physics Simulations) Unlike in other physics communities, there have been no high-performance "community codes" available to study strongly correlated quantum systems. Driven by a common believe that implementations of numerical methods should be publicly available to the physics community as open source codes we have built a common framework to integrate and publish codes for numerical simulations of strongly correlated systems and in 2003 launched the ALPS project (Algorithms and Libraries for Physics Simulations). Today the ALPS project is maintained by an international collaboration of researchers [1-4] and widely used by condensed matter theorists and experimentalists around the globe. Besides contributing implementations of several applications and basic libraries - most notably the worm algorithm for continuous-time quantum Monte Carlo simulations [5] - we have co-organized a series of workshops where the ALPS project was founded. On the ALPS webpages you can find a description of our ongoing and past projects.

References
[1] F. Alet et al. (ALPS collaboration), J. Phys. Soc. Jpn. Suppl. 74, 30 (2005).
[2] A. F. Albuquerque et al. (ALPS collaboration), J. Magn. Mag. Mat. 310, 1187 (2007).
[3] B. Bauer et al. (ALPS collaboration), J. Stat. Mech. P05001 (2011).

 Other resources
[4] Slides form a talk on The ALPS Project: Open Source Software for Quantum Lattice Models
[5] Slides form a talk on The worm algorithm
[6] Slides form a talk on Series expansions for Quantum Lattice Models


Interacting non-Abelian anyons

Topological quantum liquids, such as fractional quantum Hall liquids, rotating Bose-Einstein condensates or px + ipy superconductors, harbor exotic quasiparticle excitations, which due to their unusual exchange statistics are referred to as anyons. A particularly intriguing species are non-Abelian anyons, which have attracted considerable interest in proposals for topological quantum computation. Their defining characteristic manifests itself when considering a set of non-Abelian anyons, which gives rise to a (degenerate) manifold of states even when pinning the anyons to fixed locations in space.

Nucleation of a topological liquid due to interactions between anyons. One line of my current research explores how this manifold of states for a set of non-Abelian anyons is split in the presence of interactions between the anyons. We could recently show that as a result of this splitting a single ground state is selected [1]. This new collective state corresponds to a gapped quantum liquid nucleated within the original parent liquid (of which the anyons are excitations) with characteristic (neutral) edge states forming at the spatial interface between the two liquids. These edge states are in precise correspondence with the gapless modes found for one-dimensional arrangements of anyons, such as the "golden chain" [2] and variations thereof [3]. This physics is at play when tuning the magnetic field off the center of the plateau for a non-Abelian quantum Hall state and will have direct experimental signatures, such as modifications to the thermal heat transport.

References
[1] A. Feiguin, S. Trebst, A. Ludwig, M. Troyer, A. Kitaev, Z. Wang, and M. Freedman, Phys. Rev. Lett. 98, 160409 (2007).
[2] S. Trebst, M. Troyer, Z. Wang and A.W.W. Ludwig, Prog. Theor. Phys. Suppl. 176, 384 (2008).
[3] S. Trebst, E. Ardonne, A. Feiguin, D. A. Huse, A. W. W. Ludwig, M. Troyer, Phys. Rev. Lett. 101, 050401 (2008).
[4] C. Gils, E. Ardonne, S. Trebst, A. W. W. Ludwig, M. Troyer, Z. Wang, Phys. Rev. Lett. 103, 070401 (2009).
[5] Eddy Ardonne, Jan Gukelberger, Andreas W.W. Ludwig, Simon Trebst, and Matthias Troyer, New J. Phys. 13, 045006 (2011).
[6] Andreas W.W. Ludwig, Didier Poilblanc, Simon Trebst, and Matthias Troyer, New J. Phys. 13, 045014 (2011).
[7] D. Poilblanc, A. Ludwig, S. Trebst, and M. Troyer, Phys. Rev. B 83, 134439 (2011).
[8] C.R. Laumann, D.A. Huse, A.W.W. Ludwig, G. Refael, S. Trebst, and M. Troyer, Phys. Rev. B 85, 224201 (2012).
[9] Chris R. Laumann, Andreas W.W. Ludwig, David A. Huse, and Simon Trebst, Phys. Rev. B 85, 161301(R) (2012).
[10] C. Gils, E. Ardonne, S. Trebst, D.A. Huse, A.W.W. Ludwig, M. Troyer, and Z. Wang, Phys. Rev. B 87, 235120 (2013).

 Other resources
[11] Slides from a talk on Interactions and Disorder in Topological Quantum Matter
[12] Slides from a talk on Collective states of interacting anyons, edge states and the nucleation of topological liquids
[13] Slides from a talk on Interacting Anyons in Topological Quantum Liquids: The Golden Chain
[14] Video and slides from an overview talk at KITP from 2009.


Optimized statistical ensembles

Competing phases or interactions in complex many-particle systems can result in free energy barriers that strongly suppress thermal equilibration. Prominent examples of slowly equilibrating systems are frustrated magnets, glasses or proteins. To study the equilibrium behavior of such systems we have developed an adaptive Monte Carlo simulation technique that is capable to explore and overcome the entropic barriers which cause the slow-down [1]. The algorithm systematically optimizes the simulated statistical ensemble in broad-histogram Monte Carlo simulations by maximizing the round-trip rates between low and high entropy states based on measurements of the local diffusivity. In contrast to flat-histogram sampling techniques which recently have become very popular we demonstrated that these optimized histogram methods do not suffer from a critical slowing down [1,2]. In fact, for a number of applications we have shown that the simulation of an optimized ensemble can speed up equilibration by orders of magnitude in systems which have long relaxation times in conventional simulations such as low-energy configurations of frustrated systems [1], Potts models (with up to 250 states) exhibiting strong first-order transitions [3], dense Lennard-Jones liquids [4] or quantum systems [5].

Room temperature structure of the chicken villin headpiece HP-36 In an interdisciplinary project we applied this technique to study the folding of small proteins [6]. It turns out that the state-of-the-art parallel tempering algorithm for these systems can be significantly improved by applying our novel approach to optimize the simulated temperature/replica set [7]. The adaptive optimization thereby reveals the multiple temperature scales governing the folding process of a single protein and systematically reallocates computational resources to the bottlenecks in the transition.

Our new algorithms have been met with some enthusiasm by the broader numerical community and are now employed in a variety of fields beyond condensed matter physics, including biological physics, chemical engineering, high-energy physics and probabilistic optimization.

For a short introductory review of the ensemble optimization techniques see references [8,9].

References
[1] Simon Trebst, David A. Huse, Matthias Troyer, Phys. Rev. E 70, 046701 (2004).
[2] P. Dayal, S. Trebst, S. Wessel, D. Würtz, M. Troyer, S. Sabhapandit, S. N. Coppersmith, Phys. Rev. Lett. 92, 097201 (2004).
[3] Bela Bauer, Emanuel Gull, Simon Trebst, Matthias Troyer, and David A. Huse, J. Stat. Mech. P01020 (2010).
[4] Simon Trebst, Emanuel Gull, Matthias Troyer, J. Chem. Phys. 123, 204501 (2005).
[5] S. Wessel, N. Stoop, E. Gull, S. Trebst, M. Troyer, J. Stat. Mech. P12005 (2007).
[6] Simon Trebst, Matthias Troyer, Ulrich H. E. Hansmann, J. Chem. Phys. 124, 174903 (2006).
[7] H.G. Katzgraber, S. Trebst, D.A. Huse, M. Troyer, J. Stat. Mech. P03018 (2006).
[8] S. Trebst et al., Springer Proceedings in Physics 123, 33 (2008).

 Other resources
[9] Video and lecture notes of an overview talk on Extended statistical ensembles given at the 2010 Boulder Summer School
[10] Slides from a review talk on Optimized statistical ensembles